Advertisements
Advertisements
प्रश्न
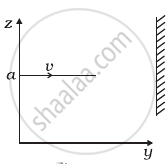
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
विकल्प
`mva hate_x`
`2mva hate_x`
`ymv hate_x`
`2ymv hate_x`
उत्तर
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is `underline(2mva hate_x)`.
Explanation:
The initial velocity is `vhati = vhate_y` and, after reflection from the wall, the final velocity is `v_f = - vhate_y`. The trajectory is described as `r = yhate_y + ahate_z`. Hence the change in angular momentum is `r xx m(v_f - v_i) = 2mvahate_x`.
APPEARS IN
संबंधित प्रश्न
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?
- The forces may be acting radially from a point on the axis.
- The forces may be acting on the axis of rotation.
- The forces may be acting parallel to the axis of rotation.
- The torque caused by some forces may be equal and opposite to that caused by other forces.
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
Angular momentum of a single particle moving with constant speed along the circular path ______.
