Advertisements
Advertisements
प्रश्न
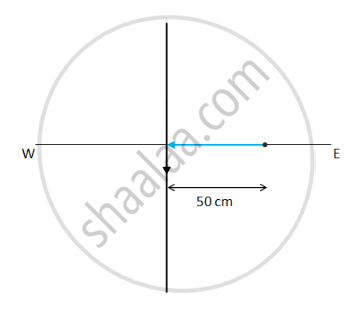
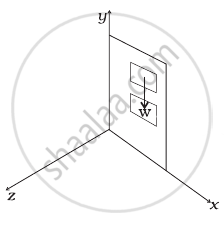
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
उत्तर
We know that
\[ \overrightarrow{\tau} = \overrightarrow{r} \times \overrightarrow{F} \]
Given:-
\[ \overrightarrow{r} = - 0 . 5 \hat i m\]
\[ \overrightarrow{F} = - mg \hat j \]
The torque becomes
\[ \overrightarrow{\tau} = 0 . 5\left( - \hat i \right) \times mg\left( - \hat j \right)\]
\[ \overrightarrow{\tau} = 0 . 5 \text{mg } \hat k \left[ \because \hat i \times \hat j = \hat k \right]\]
No, there will be no angular acceleration on the particle due to the torque.
Angular acceleration is given by \[\alpha = \frac{\tau}{I}\]. As the particle here moves in a straight line, the centre of rotation lies at a distance infinity \[(r = \infty );\] so, moment of inertia \[(I = m r^2 )\] of the particle is infinity.
\[ \therefore \alpha = 0\]
APPEARS IN
संबंधित प्रश्न
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
Define torque and mention its unit.
State conservation of angular momentum.
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
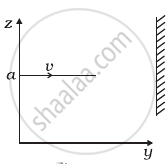
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
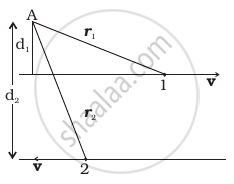
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
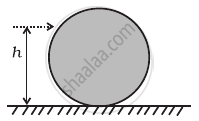
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
