Advertisements
Advertisements
प्रश्न
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
उत्तर
\[\text{No, }\overrightarrow r \times \overrightarrow \tau || \overrightarrow \Gamma\text{ is not true.} \]
In fact, it is never true.This is because:
\[ \overrightarrow r \times \overrightarrow \tau \]
\[ = \overrightarrow r \times \left( \overrightarrow r \times \overrightarrow F \right)\]
Applying vector triple product, we get:
\[\overrightarrow r \times \left( \overrightarrow r \times \overrightarrow F \right)\]
\[ = \left(\overrightarrow r . \overrightarrow F \right) \overrightarrow r - \left( \overrightarrow r . \overrightarrow r \right) \overrightarrow F \]
\[ \because \overrightarrow r . \overrightarrow r = r^2 \]
\[ = \left( \overrightarrow r . \overrightarrow F \right) \overrightarrow r {}^{-r^2} \overrightarrow F \]
\[\text{If }\overrightarrow r . \overrightarrow F = 0; \text{ that is, }\overrightarrow r {}^{\perp}\overrightarrow F,\text{ then} \]
\[\overrightarrow r \times \overrightarrow \Gamma = {}^{-r^2}\overrightarrow F \]
\[\text{We know that }r^2\text{ is never negative and }\overrightarrow r \times \overrightarrow \Gamma = -r^2 \overrightarrow F \]
This implies that both vectors may be antiparallel to each other but not parallel.
APPEARS IN
संबंधित प्रश्न
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
The torque of the weight of any body about any vertical axis is zero. If it always correct?
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

Calculate the total torque acting on the body shown in the following figure about the point O.

A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
What are the conditions in which force can not produce torque?
State conservation of angular momentum.
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
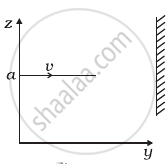
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?
- The forces may be acting radially from a point on the axis.
- The forces may be acting on the axis of rotation.
- The forces may be acting parallel to the axis of rotation.
- The torque caused by some forces may be equal and opposite to that caused by other forces.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
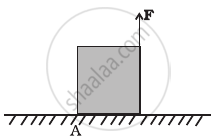
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
