Advertisements
Advertisements
Question
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
Solution
\[\text{No, }\overrightarrow r \times \overrightarrow \tau || \overrightarrow \Gamma\text{ is not true.} \]
In fact, it is never true.This is because:
\[ \overrightarrow r \times \overrightarrow \tau \]
\[ = \overrightarrow r \times \left( \overrightarrow r \times \overrightarrow F \right)\]
Applying vector triple product, we get:
\[\overrightarrow r \times \left( \overrightarrow r \times \overrightarrow F \right)\]
\[ = \left(\overrightarrow r . \overrightarrow F \right) \overrightarrow r - \left( \overrightarrow r . \overrightarrow r \right) \overrightarrow F \]
\[ \because \overrightarrow r . \overrightarrow r = r^2 \]
\[ = \left( \overrightarrow r . \overrightarrow F \right) \overrightarrow r {}^{-r^2} \overrightarrow F \]
\[\text{If }\overrightarrow r . \overrightarrow F = 0; \text{ that is, }\overrightarrow r {}^{\perp}\overrightarrow F,\text{ then} \]
\[\overrightarrow r \times \overrightarrow \Gamma = {}^{-r^2}\overrightarrow F \]
\[\text{We know that }r^2\text{ is never negative and }\overrightarrow r \times \overrightarrow \Gamma = -r^2 \overrightarrow F \]
This implies that both vectors may be antiparallel to each other but not parallel.
APPEARS IN
RELATED QUESTIONS
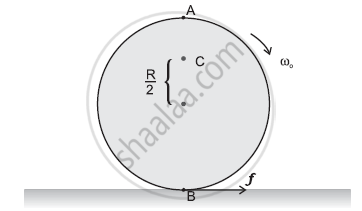
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
State conservation of angular momentum.
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
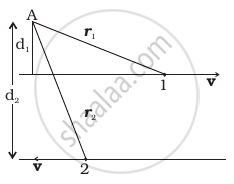
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
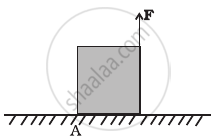
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
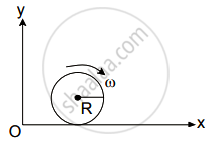
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
Angular momentum of a single particle moving with constant speed along the circular path ______.
A solid sphere is rotating in free space. If the radius of the sphere is increased while keeping the mass the same, which one of the following will not be affected?
