Advertisements
Advertisements
Question
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
Solution
a. As there is no net external torque on the system, the law of conservation of angular momentum may be applied.
Gravitational forces and their normal reactions are external forces, but their net torque is zero, therefore they have no impact.
b. By applying the Law of conversation of angular momentum,
`L_j = L_i`
⇒ `I_ω = I_1ω_1 + I_2ω_2`
I = moment of inertia
ω = angular speed
∴ ω = `(I_1ω_1 + ω_2ω_2)/I` ∴ I = I1 + I2
∴ ω = `(I_1ω_1 + ω_2ω_2)/I`
c. As `KE_f = KE_R + KE_T`
Translational Energy = 0
∴ KET = 0
∴ `KE_f = KE_R = 1/2 Iω^2 = 1/2 (I_1 + I_2) [(I_1ω_1 + I_2ω_2)/(I_1 + I_2)]^2`
`KE_f = 1/2 (I_1ω_1 + I_2ω_2)^2/((I_1 + I_2))`
`KE_i = KE_(1R) + KE_(2R) + KE_(1T) + KE_(2T)`
Because there is no translational motion which in turn results,
KE1T = 0
KE2T = 0
∴ `KE_i = 1/2 I_1ω_1^2 + 1/2 I_2ω_2^2 = 1/2 (I_1ω_1^2 + I_2ω_2^2)`
∴ `ΔKE = KE_f - KE_i = 1/2 (I_1ω_1 + I_2ω_2)^2/((I_1 + I_2)) - 1/2 (I_1ω_1^2 + I_2ω_2^2)`
= `1/2 [(I_1^2ω_1^2 + I_2^2ω_2^2 + 2I_1I_2ω_1ω_2 - [(I_1 + I_2)(I_1ω_1^2 + I_2w_2^2)]]/(I_1 + I_2)]`
= `[([I_1^2ω_1^2 + I_2^2ω_2^2 + 2I_1I_2ω_1ω_2] - [I_1^2ω_1^2 + I_2^2ω_2^2 + I_1I_2ω_1^2 + I_2^2ω_2^2])/(2(I_1 + I_2))]`
= `(-I_1I_2)/(2(I_1 + I_2)) (-2ω_1ω_2 + ω_2^2 + ω_1^2)`
ΔKE = `(-I_1I_2)/(2(I_1 + I_2)) (ω_1 - ω_2)^2 < 0`
d. `K_f < K_i` since energy is wasted due to friction between discs' moving surfaces.
APPEARS IN
RELATED QUESTIONS
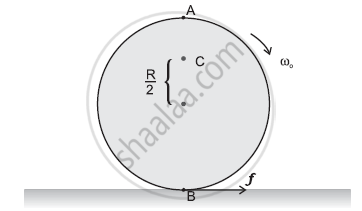
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
State conservation of angular momentum.
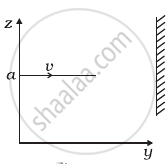
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
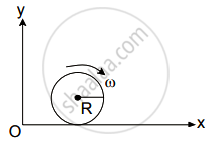
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
A solid sphere is rotating in free space. If the radius of the sphere is increased while keeping the mass the same, which one of the following will not be affected?
