Advertisements
Advertisements
Question
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
Solution
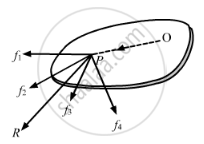
\[\text{Let } \overrightarrow{f_1},\overrightarrow{f_2},\overrightarrow{f_3},....\overrightarrow{f_n}\text{ be the forces acting on a point P.}\]
Let O be the point along which torques \(moments) will be taken.
Let:-
\[ \overrightarrow{f_1} + \overrightarrow{f_2} + \overrightarrow{f_3} + . . . + \overrightarrow{f_n} = \overrightarrow{R}..............(1)\]
Moments of force (torque) \[\overrightarrow{f_i}\] about O will be
\[ \overrightarrow{\tau_1} = \overrightarrow{OP} \times \overrightarrow{f_1} \]
The sum of the torques about O will be
\[ \overrightarrow{M} = \overrightarrow{OP} \times \overrightarrow{f_1} + \overrightarrow{OP} \times \overrightarrow{f_2} + . . . + \overrightarrow{OP} \times \overrightarrow{f_n} \]
\[ \Rightarrow \overrightarrow{M} = \overrightarrow{OP} \times \left( \overrightarrow{f_1} + \overrightarrow{f_2} + \overrightarrow{f_3} + . . . + \overrightarrow{f_n} \right)\]
\[ \Rightarrow \overrightarrow{M} = \overrightarrow{OP} \times \overrightarrow{R}...............\left[\text{From (1)}\right]\]
Thus, we see that the torque of the resultant force \[\overrightarrow{R}\] of the forces \[\overrightarrow{f_1},\overrightarrow{f_2},\overrightarrow{f_3},.....,\overrightarrow{f_n} \] gives the sum of the moments of the torques.
APPEARS IN
RELATED QUESTIONS
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
The torque of the weight of any body about any vertical axis is zero. If it always correct?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
Define torque and mention its unit.
What are the conditions in which force can not produce torque?
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
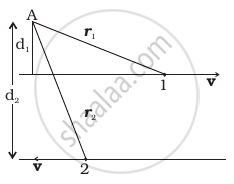
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
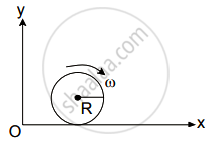
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
The magnitude of the torque on a particle of mass 1 kg is 2.5 Nm about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians) ______.
