Advertisements
Advertisements
प्रश्न
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
उत्तर
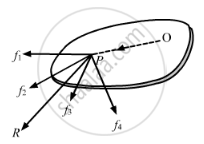
\[\text{Let } \overrightarrow{f_1},\overrightarrow{f_2},\overrightarrow{f_3},....\overrightarrow{f_n}\text{ be the forces acting on a point P.}\]
Let O be the point along which torques \(moments) will be taken.
Let:-
\[ \overrightarrow{f_1} + \overrightarrow{f_2} + \overrightarrow{f_3} + . . . + \overrightarrow{f_n} = \overrightarrow{R}..............(1)\]
Moments of force (torque) \[\overrightarrow{f_i}\] about O will be
\[ \overrightarrow{\tau_1} = \overrightarrow{OP} \times \overrightarrow{f_1} \]
The sum of the torques about O will be
\[ \overrightarrow{M} = \overrightarrow{OP} \times \overrightarrow{f_1} + \overrightarrow{OP} \times \overrightarrow{f_2} + . . . + \overrightarrow{OP} \times \overrightarrow{f_n} \]
\[ \Rightarrow \overrightarrow{M} = \overrightarrow{OP} \times \left( \overrightarrow{f_1} + \overrightarrow{f_2} + \overrightarrow{f_3} + . . . + \overrightarrow{f_n} \right)\]
\[ \Rightarrow \overrightarrow{M} = \overrightarrow{OP} \times \overrightarrow{R}...............\left[\text{From (1)}\right]\]
Thus, we see that the torque of the resultant force \[\overrightarrow{R}\] of the forces \[\overrightarrow{f_1},\overrightarrow{f_2},\overrightarrow{f_3},.....,\overrightarrow{f_n} \] gives the sum of the moments of the torques.
APPEARS IN
संबंधित प्रश्न
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
Calculate the total torque acting on the body shown in the following figure about the point O.

A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
Define torque and mention its unit.
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
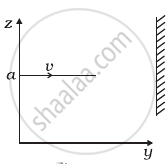
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
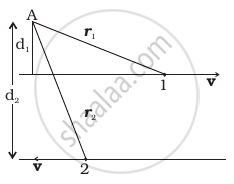
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
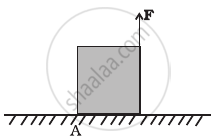
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
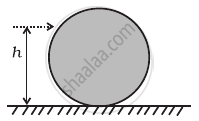
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
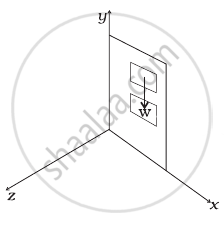
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
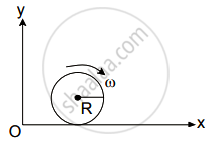
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
