Advertisements
Advertisements
प्रश्न
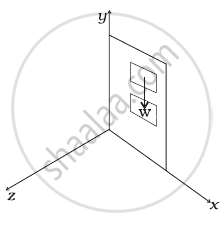
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
उत्तर
According to the diagram, where weight of the door acts along the negative y-axis.
Torque is not produced by weight about the y-axis.
Because the direction of weight is parallel to the y-axis (axis of rotation).
A force can produce torque only along the direction normal to itself because f = r × F. So when the door is in the xy-plane, the torque produced by gravity can only be along ±z-direction never about an axis passing through the y-direction.
Hence, the weight will not produce any torque about the y-axis.
APPEARS IN
संबंधित प्रश्न
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
A simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight ω of the bob about the point of suspension. When is the torque zero?
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
What are the conditions in which force can not produce torque?
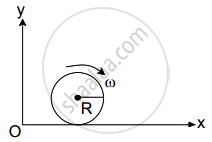
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
