Advertisements
Advertisements
प्रश्न
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
विकल्प
`1/4I(omega_1 - omega_2)^2`
`I(omega_1 - omega_2)^2`
`1/8I(omega_1 - omega_2)^2`
`1/2I(omega_1 - omega_2)^2`
उत्तर
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, `underline(1/4I(omega_1 - omega_2)^2)`.
APPEARS IN
संबंधित प्रश्न
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
What are the conditions in which force can not produce torque?
Choose the correct alternatives:
- For a general rotational motion, angular momentum L and angular velocity ω need not be parallel.
- For a rotational motion about a fixed axis, angular momentum L and angular velocity ω are always parallel.
- For a general translational motion , momentum p and velocity v are always parallel.
- For a general translational motion, acceleration a and velocity v are always parallel.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
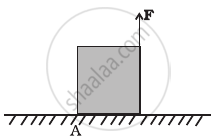
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
A particle of mass 'm' is moving in time 't' on a trajectory given by
`vecr = 10alphat^2hati + 5beta(t - 5)hatj`
Where α and β are dimensional constants.
The angular momentum of the particle becomes the same as it was for t = 0 at time t = ______ seconds.
