Advertisements
Advertisements
प्रश्न
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
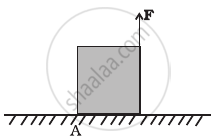
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
उत्तर
| (a) mg/4 < F < mg/2 | (ii) Cube will not exhibit motion. |
| (b) F > mg/2 | (iii) Cube will begin to rotate and slip at A. |
| (c) F > mg | (i) Cube will move up. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
Explanation:
Consider the below diagram
Moment of the force F about point A, τ1 = F × a .....(anti-clockwise)
Moment of weight mg of the cube about point A.
τ2 = `mg xx a/2` .....(clockwise)
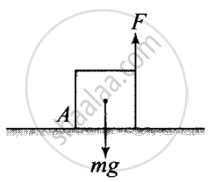
Cube will not exhibit motion, If τ1 = τ2 ......(∵ In this case, both the torque will cancel the effect of each other)
∴ F × a = `mg xx a/2`
⇒ F = `(mg)/2`
Cube will rotate only when, τ1 > τ2
⇒ F × a > `mg xx a/2`
⇒ `F > (mg)/2`
Let the normal reaction is acting at `a/3` from point A, then
`mg xx a/3 = F xx a` or `F = (mg)/3` .......(For no motion)
When F = `(mg)/4` which is less than `(mg)/3`, .....`(F < (mg)/3)`
There will be no motion.
APPEARS IN
संबंधित प्रश्न
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
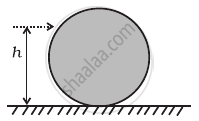
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
Angular momentum of a single particle moving with constant speed along the circular path ______.
