Advertisements
Advertisements
Question
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
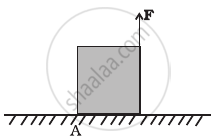
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
Advertisements
Solution
| (a) mg/4 < F < mg/2 | (ii) Cube will not exhibit motion. |
| (b) F > mg/2 | (iii) Cube will begin to rotate and slip at A. |
| (c) F > mg | (i) Cube will move up. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
Explanation:
Consider the below diagram
Moment of the force F about point A, τ1 = F × a .....(anti-clockwise)
Moment of weight mg of the cube about point A.
τ2 = `mg xx a/2` .....(clockwise)
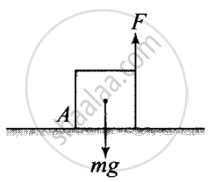
Cube will not exhibit motion, If τ1 = τ2 ......(∵ In this case, both the torque will cancel the effect of each other)
∴ F × a = `mg xx a/2`
⇒ F = `(mg)/2`
Cube will rotate only when, τ1 > τ2
⇒ F × a > `mg xx a/2`
⇒ `F > (mg)/2`
Let the normal reaction is acting at `a/3` from point A, then
`mg xx a/3 = F xx a` or `F = (mg)/3` .......(For no motion)
When F = `(mg)/4` which is less than `(mg)/3`, .....`(F < (mg)/3)`
There will be no motion.
APPEARS IN
RELATED QUESTIONS
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
What are the conditions in which force can not produce torque?
State conservation of angular momentum.
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
Choose the correct alternatives:
- For a general rotational motion, angular momentum L and angular velocity ω need not be parallel.
- For a rotational motion about a fixed axis, angular momentum L and angular velocity ω are always parallel.
- For a general translational motion , momentum p and velocity v are always parallel.
- For a general translational motion, acceleration a and velocity v are always parallel.
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?
- The forces may be acting radially from a point on the axis.
- The forces may be acting on the axis of rotation.
- The forces may be acting parallel to the axis of rotation.
- The torque caused by some forces may be equal and opposite to that caused by other forces.
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
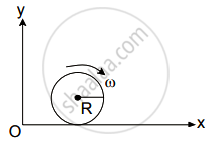
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms−1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
