Advertisements
Advertisements
प्रश्न
Calculate the total torque acting on the body shown in the following figure about the point O.

उत्तर
Torque about a point = Total force × Perpendicular distance
Let the anticlockwise torque and clockwise acting torque be positive and negative, respectively.
Torque at O due to 5 N force is zero as it is passing through O.
Torque at O due to 15 N force,
\[\tau_1 = 15 \times 6 \times {10}^{- 2} \times \sin37^\circ\]
\[ = 15 \times 6 \times {10}^{- 2} \times \frac{3}{5}\]
\[ = 0 . 54 N - m .........\left(\text{anticlockwise} \right)\]
Torque at O due to 10 N force,
\[\tau_2 = 10 \times 4 \times {10}^{- 2} = 0 . 4 N - m ........\left(\text{clockwise} \right)\]
Torque at O due to 20 N force,
\[\tau_3 = 20 \times 4 \times {10}^{- 2} \times \sin30^\circ\]
\[ = 20 \times 4 \times {10}^{- 2} \times \frac{1}{2}\]
\[ = 0 . 4 N - m .........\left(\text{Anticlockwise} \right)\]
Resultant torque acting at O,
\[\tau = \left( 0 . 54 - 0 . 4 + 0 . 4 \right)\]
\[ = 0 . 54 N - m \left(\text{Anticlockwise} \right)\]
APPEARS IN
संबंधित प्रश्न
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
The torque of the weight of any body about any vertical axis is zero. If it always correct?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
Define torque and mention its unit.
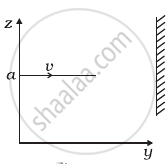
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
A solid sphere is rotating in free space. If the radius of the sphere is increased while keeping the mass the same, which one of the following will not be affected?
