Advertisements
Advertisements
प्रश्न
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
विकल्प
angular acceleration
angular velocity when the rod completes one rotation
angular momentum when the rod completes one rotation
torque of the applied force
उत्तर
torque of the applied force
The torque of the applied force does not depend on the density of a rod. It depend on the distance between the pivot and the point where F is applied. So, it does not depend on which end of the rod is pivoted.
APPEARS IN
संबंधित प्रश्न
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

Calculate the total torque acting on the body shown in the following figure about the point O.

A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
What are the conditions in which force can not produce torque?
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
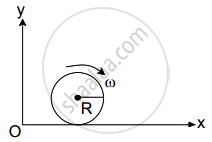
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
