Advertisements
Advertisements
प्रश्न
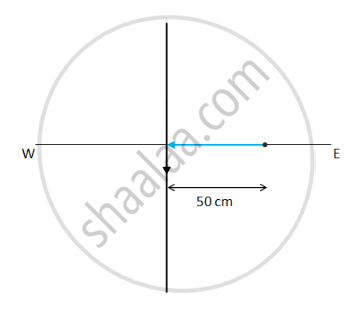
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
उत्तर
We know that
\[ \overrightarrow{\tau} = \overrightarrow{r} \times \overrightarrow{F} \]
Given:-
\[ \overrightarrow{r} = - 0 . 5 \hat i m\]
\[ \overrightarrow{F} = - mg \hat j \]
The torque becomes
\[ \overrightarrow{\tau} = 0 . 5\left( - \hat i \right) \times mg\left( - \hat j \right)\]
\[ \overrightarrow{\tau} = 0 . 5 \text{mg } \hat k \left[ \because \hat i \times \hat j = \hat k \right]\]
No, there will be no angular acceleration on the particle due to the torque.
Angular acceleration is given by \[\alpha = \frac{\tau}{I}\]. As the particle here moves in a straight line, the centre of rotation lies at a distance infinity \[(r = \infty );\] so, moment of inertia \[(I = m r^2 )\] of the particle is infinity.
\[ \therefore \alpha = 0\]
APPEARS IN
संबंधित प्रश्न
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

Calculate the total torque acting on the body shown in the following figure about the point O.

A cubical block of mass m and edge a slides down a rough inclined plane of inclination θ with a uniform speed. Find the torque of the normal force acting on the block about its centre.
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
Define torque and mention its unit.
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
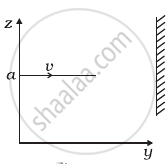
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
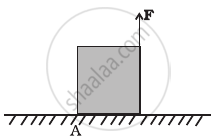
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
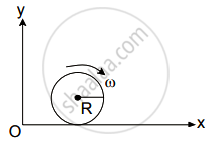
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
A rod of mass 'm' hinged at one end is free to rotate in a horizontal plane. A small bullet of mass m/4 travelling with speed 'u' hits the rod and attaches to it at its centre. Find the angular speed of rotation of rod just after the bullet hits the rod 3. [take length of the rod as 'l']
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
