Advertisements
Advertisements
Question
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
Solution
Let M and R be the mass and radius of the half-disc, mass per unit area of the half-disc
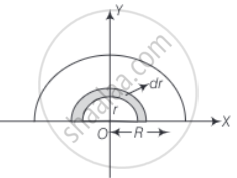
(a) The half-disc can be supposed to be consists of a large number of semicircular rings of mass om and thickness and radii ranging from r = 0 to r = R.
The surface area of the semicircular ring of radius r and of thickness dr = `1/2 2πr xx dr = πrdr`
∴ Mass of this elementary ring, dm = `πrdr xx (2M)/(rR^2)`
dm = `(2M)/R^2 rdr`
If (x, y) are coordinates of the centre of mass of this element,
Then, `(x, y) = (0, (2r)/π)`
Therefore, x = 0 and y = `(2r)/π`
Let xCM and yCM be the coordinates of the centre of mass of the semicircular disc.
Then xCM = `1/M int_0^R xdm = 1/M int_0^R 0 dm = 0`
yCM = `1/M int_0^R ydm = 1/M int_0^R (2r)/π xx ((2M)/R^2 rdr)`
= `4/(πR^2) int_0^R r^2dr`
= `4/(πR^2) [r^3/3]_0^R`
= `4/(πR^2) xx (R^3/3 - 0)`
= `(4R)/(3π)`
∴ Centre of mass of the semicircular disc = `(0, (4R)/(3π))`
(b) Centre of mass of a uniform quarter disc.
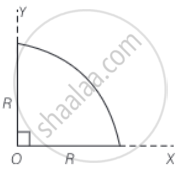
Mass per unit area of the quarter disc = `M/((πR^2)/4) = (4M)/(πR^2)`
Using symmetry
For a half-disc along the y-axis centre of mass will be at `x = (4R)/(3π)`
For a half-disc along the x-axis centre of mass will be at `x = (4R)/(3π)`
Hence, for the quarter disc centre of mass = `((4R)/(3π), (4R)/(3π))`
APPEARS IN
RELATED QUESTIONS
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.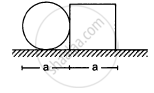
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
The centre of mass of a system of two particles divides the distance between them ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
