Question

Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.

Answer 1

Let M and R be the mass and radius of the half-disc, mass per unit area of the half-disc

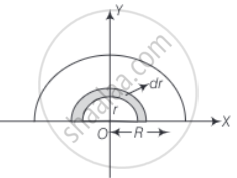
(a) The half-disc can be supposed to be consists of a large number of semicircular rings of mass om and thickness and radii ranging from r = 0 to r = R.

The surface area of the semicircular ring of radius r and of thickness dr = `1/2 2πr xx dr = πrdr`

 ∴ Mass of this elementary ring, dm = `πrdr xx (2M)/(rR^2)`

dm = `(2M)/R^2 rdr`

If (x, y) are coordinates of the centre of mass of this element,

Then, `(x, y) = (0, (2r)/π)`

Therefore, x = 0 and y = `(2r)/π`

Let x_CM and y_CM be the coordinates of the centre of mass of the semicircular disc.

Then x_CM = `1/M int_0^R xdm = 1/M int_0^R 0  dm = 0`

 y_CM = `1/M int_0^R ydm = 1/M int_0^R (2r)/π xx ((2M)/R^2  rdr)`

= `4/(πR^2) int_0^R r^2dr`

= `4/(πR^2) [r^3/3]_0^R`

= `4/(πR^2) xx (R^3/3 - 0)`

= `(4R)/(3π)`

∴ Centre of mass of the semicircular disc = `(0, (4R)/(3π))`

(b) Centre of mass of a uniform quarter disc.

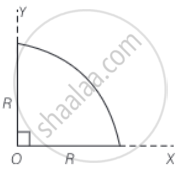
Mass per unit area of the quarter disc = `M/((πR^2)/4) = (4M)/(πR^2)`

Using symmetry

For a half-disc along the y-axis centre of mass will be at `x = (4R)/(3π)`

For a half-disc along the x-axis centre of mass will be at `x = (4R)/(3π)`

Hence, for the quarter disc centre of mass = `((4R)/(3π), (4R)/(3π))`