Advertisements
Advertisements
प्रश्न
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
उत्तर
Let M and R be the mass and radius of the half-disc, mass per unit area of the half-disc
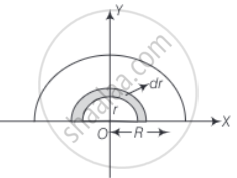
(a) The half-disc can be supposed to be consists of a large number of semicircular rings of mass om and thickness and radii ranging from r = 0 to r = R.
The surface area of the semicircular ring of radius r and of thickness dr = `1/2 2πr xx dr = πrdr`
∴ Mass of this elementary ring, dm = `πrdr xx (2M)/(rR^2)`
dm = `(2M)/R^2 rdr`
If (x, y) are coordinates of the centre of mass of this element,
Then, `(x, y) = (0, (2r)/π)`
Therefore, x = 0 and y = `(2r)/π`
Let xCM and yCM be the coordinates of the centre of mass of the semicircular disc.
Then xCM = `1/M int_0^R xdm = 1/M int_0^R 0 dm = 0`
yCM = `1/M int_0^R ydm = 1/M int_0^R (2r)/π xx ((2M)/R^2 rdr)`
= `4/(πR^2) int_0^R r^2dr`
= `4/(πR^2) [r^3/3]_0^R`
= `4/(πR^2) xx (R^3/3 - 0)`
= `(4R)/(3π)`
∴ Centre of mass of the semicircular disc = `(0, (4R)/(3π))`
(b) Centre of mass of a uniform quarter disc.
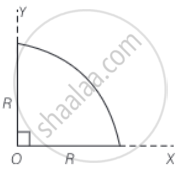
Mass per unit area of the quarter disc = `M/((πR^2)/4) = (4M)/(πR^2)`
Using symmetry
For a half-disc along the y-axis centre of mass will be at `x = (4R)/(3π)`
For a half-disc along the x-axis centre of mass will be at `x = (4R)/(3π)`
Hence, for the quarter disc centre of mass = `((4R)/(3π), (4R)/(3π))`
APPEARS IN
संबंधित प्रश्न
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
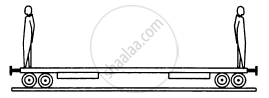
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
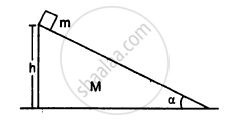
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
In rotational motion of a rigid body, all particles move with ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Which of the following statements are correct?
