Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
उत्तर
It is given that the force on both the blocks is F.
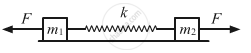
Let x1 and x2 be the extensions of blocks m1 and m2 respectively.
Total work done by the forces on the blocks = Fx1 + Fx2 ...(1)
∴ Increase in the potential energy of spring = \[\left( \frac{1}{2} \right)K( x_1 + x_2 )^2 . . . (2)\]
\[\text{ Equating the equations (1) and (2), we get: } \]
\[ \Rightarrow ( x_1 + x_2 ) = \left( \frac{2F}{k} \right) \ldots(3)\]
As the net external force on the system is zero, the centre of mass does not shift.
\[\therefore m_1 x_1 = m_2 x_2 . . . (4)\]
\[\text{ Using the equations }\left( 3 \right) \text{ and } \left( 4 \right), \text{ we get}: \]
\[ \frac{m_1}{m_2} x_1 + x_1 = \frac{2F}{k}\]
\[ \Rightarrow x_1 \left( 1 + \frac{m_1}{m_2} \right) = \frac{2F}{k}\]
\[ \Rightarrow x_1 = \frac{2F m_2}{k( m_1 + m_2 )}\]
Similarly,
\[x_2 = \frac{2F m_1}{k( m_1 + m_2 )}\]
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
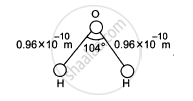
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
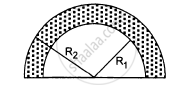
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
In an elastic collision
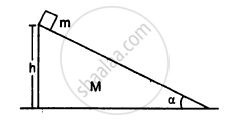
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
The centre of mass of a system of two particles divides the distance between them ______.
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
