Advertisements
Advertisements
प्रश्न
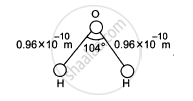
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
उत्तर
Let OX be the x-axis, OY be the Y-axis and O be the origin. 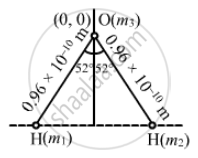
\[\text{ Mass of O atom, m}_1 = 16 \text{unit }\]
Let the position of oxygen atom be origin.
\[\Rightarrow x_1 = y_1 = 0\]
\[\text{ Mass of H atom ,m}_2 = 1 \text{unit}\]
\[ x_2 = - 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_2 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ\]
\[\text{Now, m}_3 = 1 \text{unit}\]
\[ x_3 = 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_3 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ \]
The X coordinate of the center of mass is given by:
\[ x_{cm} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 1 \times \left( - 0 . 96 \times {10}^{- 10} \sin 52^\circ\right) + 1 \times 0 . 96 \times {{10}^-}^{10} \sin 52^\circ] }{1 + 1 + 16} = 0\]
\[\text{ The Y coordinate of the center of mass is given by: }\]
\[ y_{cm} = \frac{m_1 y_1 + m_2 y_2 + m_3 y_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{1 + 1 + 16}\]
\[ = \frac{2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{18}\]
\[ = 6 . 4 \times {10}^{- 12} \text{m}\]
Hence, the distance of centre of mass of the molecule from the centre of the oxygen atom is (\[ = 6 . 4 \times {10}^{- 12} \text{m}\]).
APPEARS IN
संबंधित प्रश्न
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
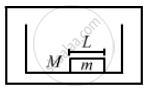
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Define centre of mass.
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
A mass of 1kg is suspended by a string. It is first lifted up with an acceleration of 4.9 m/s2 and then lowered down with same acceleration. The ratio of tensions in the string in the two cases, respectively is g = 9.8 m/s2 ______.
In rotational motion of a rigid body, all particles move with ______.
Centre of mass is a point ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following statements are correct?
For which of the following does the centre of mass lie outside the body?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
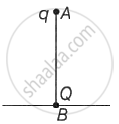
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.