Advertisements
Advertisements
Question
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
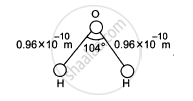
Solution
Let OX be the x-axis, OY be the Y-axis and O be the origin. 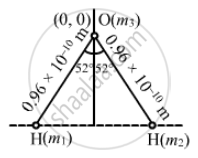
\[\text{ Mass of O atom, m}_1 = 16 \text{unit }\]
Let the position of oxygen atom be origin.
\[\Rightarrow x_1 = y_1 = 0\]
\[\text{ Mass of H atom ,m}_2 = 1 \text{unit}\]
\[ x_2 = - 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_2 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ\]
\[\text{Now, m}_3 = 1 \text{unit}\]
\[ x_3 = 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_3 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ \]
The X coordinate of the center of mass is given by:
\[ x_{cm} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 1 \times \left( - 0 . 96 \times {10}^{- 10} \sin 52^\circ\right) + 1 \times 0 . 96 \times {{10}^-}^{10} \sin 52^\circ] }{1 + 1 + 16} = 0\]
\[\text{ The Y coordinate of the center of mass is given by: }\]
\[ y_{cm} = \frac{m_1 y_1 + m_2 y_2 + m_3 y_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{1 + 1 + 16}\]
\[ = \frac{2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{18}\]
\[ = 6 . 4 \times {10}^{- 12} \text{m}\]
Hence, the distance of centre of mass of the molecule from the centre of the oxygen atom is (\[ = 6 . 4 \times {10}^{- 12} \text{m}\]).
APPEARS IN
RELATED QUESTIONS
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
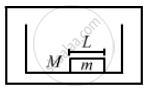
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
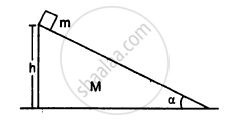
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
For which of the following does the centre of mass lie outside the body?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
