Advertisements
Advertisements
Question
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Solution
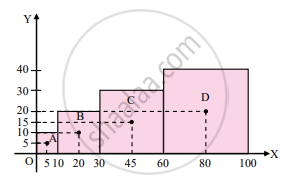
The given cubes are arranged as shown in the figure. Let one of the corners of the smallest cube lie at the origin.
As the cubes are uniform, let their center of masses lie at their respective centers.
∴ rA ≡ (5, 5), rB ≡ (20, 10), rC ≡ (45, 15) and rD ≡ (80, 20)
Also, masses of the cubes are,
`"m"_"A" = l_"A"^3 xx rho = 10^3rho`
`"m"_"B" = (20)^3 rho`
`"m"_"C" = (30)^3 rho`
`"m"_"D" = (40)^3 rho`
As the cubes are uniform, ρ is same for all of them.
∴ For X co-ordinate of centre of mass of the system,
`"X"_"cm" = (sum "m"_"i""x"_"i")/"M"`
`= ("m"_"A""x"_"A" + "m"_"B""x"_"B" + "m"_"C""x"_"C" + "m"_"D""x"_"D")/("m"_"A" + "m"_"B" + "m"_"c" + "m"_"D")`
`= ([10^3 xx rho xx 5] + [20^3 xx rho xx 20] + [30^3 xx rho xx 45] + [40^3 xx rho xx 80])/(10^3 xx rho + 20^3 xx rho + 30^3 xx rho + 40^3 xx rho)`
`= 6500/100`
= 65 cm
Similarly, Y - co-ordinate of centre of mass of system is,
`"Y"_"cm" = (sum "m"_"i""y"_"i")/"M"`
`= ("m"_"A""y"_"A" + "m"_"B""y"_"B" + "m"_"C""y"_"C" + "m"_"D""y"_"D")/("m"_"A" + "m"_"B" + "m"_"c" + "m"_"D")`
`= (10^3 xx (1 xx 5 + 8 xx 10 + 27 xx 15 + 64 xx 20))/(10^3 xx (1 + 8 + 27 + 64))`
`= 1770/100`
= 17.7 cm
Centre of mass of the system is located at point (65 cm, 17.7 cm).
APPEARS IN
RELATED QUESTIONS
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 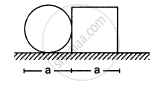
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.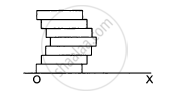
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
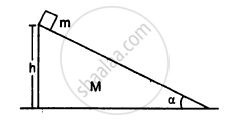
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
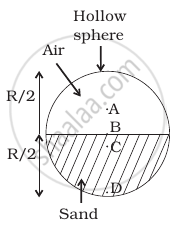
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
The centre of mass of a system of two particles divides the distance between them ______.
Which of the following has maximum momentum?
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
In rotational motion of a rigid body, all particles move with ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
