Advertisements
Advertisements
Question
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 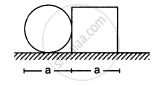
Options
inside the circular plate
inside the square plate
at the point of contact
outside the system.
Solution
inside the square plate
Let m1 be the mass of circular plate and m2 be the mass of square plate.
The thickness of both the plates is t.
\[\text{ mass = density × volume}\]
\[ m_1 = \rho\pi \left( \frac{d}{2} \right)^2 t \]
\[ m_2 = \rho d^2 t\]
Centre of mass of the circular plate lies at its centre.
Let the centre of circular plate be the origin.
\[\vec{r}_1 = 0\]
Centre of mass of the square plate lies at its centre.
\[\vec{r}_2 = 2d\]
\[\text{Now,} \]
\[R = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1 + m_2}\]
\[ = \frac{m_1 \times 0 + \rho d^2 t \times 2d}{\rho\pi \left( \frac{d}{2} \right)^2 t + \rho d^2 t}\]
\[ = \frac{2d}{\frac{\pi}{4} + 1} = 1 . 12d\]
\[ \Rightarrow \text{R > d}\]
\[\therefore\] Centre of mass of the system lies in the square plate.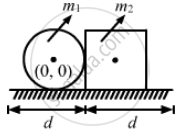
APPEARS IN
RELATED QUESTIONS
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
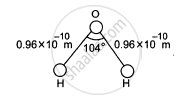
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following statements are correct?
Which of the following points is the likely position of the centre of mass of the system shown in figure?
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
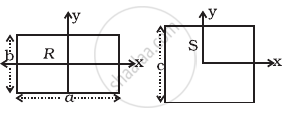
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
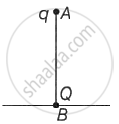
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.