Advertisements
Advertisements
Question
Solve the following problem.
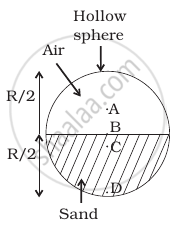
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
Solution
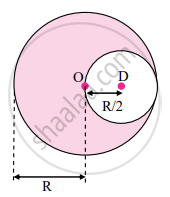
Let the centre of the sphere be origin O. Then, r1 be the position vector of the centre of mass of uniform solid sphere and r2 be the position vector of the centre of mass of the cut-out part of the sphere.
Now, mass of the sphere is given as,
M = `(4/3 pi"R"^3)rho` ....(i)
Hence, the mass of the cut part of the sphere will be,
M' = `[4/3 pi("R"/2)^3]rho` .....(∵ sphere is uniform, ρ = constant)
∴ M' = `(4/3 pi"R"^3)rho xx 1/8`
`= "M"/8` ....[From (i)]
From figure, r1 = 0, r2 = `"R"/2`
∴ Position vector of centre of mass of remaining part,
`"r"_"cm" = ("M" xx "r"_1 - "M'" xx "r"_2)/("M" - "M'")`
`= ("M" xx 0 - ("M"/8) xx "R"/2)/("M" - "M"/8)`
`= ((- "RM")/16 xx 8/"7M")`
`"r"_"cm" = (-"R")/14`
(Negative sign indicates the distance is on left side of the origin.)
Position of centre of mass of remaining sphere is `(-"R")/14`
APPEARS IN
RELATED QUESTIONS
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 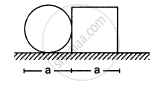
In an elastic collision
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.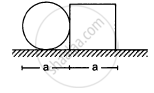
Calculate the velocity of the centre of mass of the system of particles shown in figure.

Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
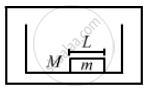
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
The centre of mass of a system of particles does not depend upon, ______
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
For which of the following does the centre of mass lie outside the body?
Which of the following points is the likely position of the centre of mass of the system shown in figure?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
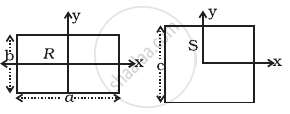
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
