Advertisements
Advertisements
Question
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
Solution
Let the two masses m1 and m2 are kept along a vertical line.
It is given that:
m1 = 10 kg
m2 = 30 kg
First block is raised through a height of 7 cm.
Thus, to raise the centre of mass by 1 cm:
\[\text{ Ycm }= \frac{m_1 y_1 + m_2 y_2}{m_1 + m_2}\]
\[ \Rightarrow 1 = \frac{10 \times 7 + 30 \times y_2}{40}\]
\[ \Rightarrow 70 + 30 y_2 = 40\]
\[ \Rightarrow 30 y_2 = - 30\]
\[ \Rightarrow y_2 = - 1\]
Therefore, the 30 kg block (m2) should be moved by 1 cm downwards in order to raise the centre of mass by 1 cm.
APPEARS IN
RELATED QUESTIONS
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
The centre of mass of a system of particles is at the origin. It follows that
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
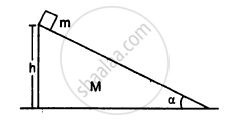
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Define centre of mass.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Which of the following statements are correct?
For which of the following does the centre of mass lie outside the body?
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
