Advertisements
Advertisements
Question
Two blocks of masses 10 kg and 20 kg are placed on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
Solution
Let the two masses m1 and m2 be placed on the X-axis.
It is given that:
m1 = 10 kg
m2 = 20 kg
The first mass is displaced by a distance of 2 cm.
\[\therefore X_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2}\]
\[ \Rightarrow X_{cm} = \frac{10 \times 2 + 20 x_2}{30}\]
As the position of the centre of mass remains unchanged,
Xcm = 0
\[\Rightarrow 0 = \frac{20 + 20 x_2}{30}\]
\[ \Rightarrow 20 + 20 x_2 = 0\]
\[ \Rightarrow 20 = - 20 x_2 \]
\[ \Rightarrow x_2 = - 1\]
Therefore, to keep the position of centre of mass unchanged, the block of mass 20 kg should be moved by a distance of 1 cm, towards left.
APPEARS IN
RELATED QUESTIONS
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous acceleration of the point of contact during rolling is zero.
A fat person is standing on a light plank floating on a calm lake. The person walks from one end to the other on the plank. His friend sitting on the shore watches him and finds that the person hardly moves any distance because the plank moves backward about the same distance as the person moves on the plank. Explain.
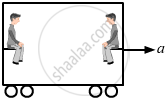
Which of the two persons shown in figure is more likely to fall down? Which external force is responsible for his falling down?
To accelerate a car we ignite petrol in the engine of the car. Since only an external force can accelerate the centre of mass, is it proper to say that "the force generated by the engine accelerates the car"?
A ball is moved on a horizontal table with some velocity. The ball stops after moving some distance. Which external force is responsible for the change in the momentum of the ball?
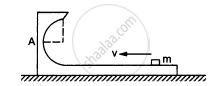
Figure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mass M placed on a horizontal floor. The curved part of the surface shown in semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.
A bullet of mass m moving at a speed v hits a ball of mass M kept at rest. A small part having mass m breaks from the ball and sticks to the bullet. The remaining ball is found to move at a speed v1 in the direction of the bullet. Find the velocity of the bullet after the collision.
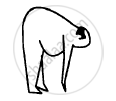
When a fat person tries to touch his toes, keeping the legs straight, he generally falls. Explain with reference to the following figure.
Solve the previous problem if the coefficient of restitution is e. \[\text{ Use } \theta = 45^\circ\, e = \frac{3}{4} \text{ and h = 5 m } .\]
A ball falls on an inclined plane of inclination θ from a height h above the point of impact and makes a perfectly elastic collision. Where will it hit the plane again?
Three identical spheres, each of mass M, are placed at the comers of a right angle triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of centre of mass.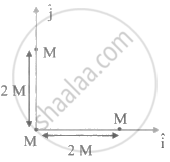
Two objects of masses 300 g and 700 g possess velocities `15 hat"i"` m/s and `4 hat"i" + 6 hat"j"` m/s respectively. The velocity of their centre of mass in m/s is:
If the net external force acting on the system of particles is zero, then which of the following may vary?
