Advertisements
Advertisements
Question
Calculate the velocity of the centre of mass of the system of particles shown in figure.

Solution
From the figure, the velocities of different masses can be written as:
\[\text{For m}_1 = 1 . 0 \text{kg}, \]
\[\text{ Velocity, } \vec{v}_1 = \left( - 1 . 5 \cos 37^\circ \hat i - 1.5 \sin 37^\circ\hat j\right) = - 1 . 2 \hat i- 0.9 \hat j\]
\[\text{For m}_2 = 1 . 2 \text{kg}, \]
\[\text{Velocity}, \vec{v}_2 = 0 . 4 \vec{j} \]
\[\text{For m}_3 = 1 . 5 \text{kg,} \]
\[\text{Velocity,} \vec{v}_3 = - 1 . 0 \cos 37^\circ \hat i0 + 1.0 \sin 37^\circ\hat j \]
\[\text{ For m}_4 = 0 . 50 \text{kg}, \]
\[\text{ Velocity,} \vec{v}_4 = 3 . 0 \hat i \]
\[\text{ For m}_5 = 1 . 0 \text{ kg}, \]
\[\text{ Velocity }, \vec{v}_5 = 2 . 0 \cos 37^\circ \hat i - 2 . 0 \sin 37^\circ \hat j \]
\[(\cos 37^\circ = \frac{4}{5} \text{ and } \sin 37^\circ \ = \frac{3}{5})\]
\[ V_{cm} = \frac{m_1 \vec{v}_1 + m_2 \vec{v}_2 + m_3 \vec{v}_3 + m_4 \vec{v}_4 + m_5 \vec{v}_5}{m_1 + m_2 + m_3 + m_4 + m_5}\]
\[ = \frac{1}{1 . 0 + 1 . 2 + 1 . 5 + 1 . 0 + 0 . 50}^\left[ 1 . 0\left( - 1 . 5 \times \frac{4}{5} \vec{i} - 1 . 5 \times \frac{3}{5} \vec{j} \right) + . . . - 2 . 0 \times \frac{3}{5} \vec{j} \right] \]
On solving the above equation, we get:
Vcm is 0.20 m/s , at 45° below the direction, towards right.
APPEARS IN
RELATED QUESTIONS
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
Which of the following statements are correct?
For which of the following does the centre of mass lie outside the body?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
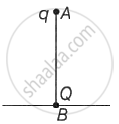
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.