Advertisements
Advertisements
प्रश्न
Calculate the velocity of the centre of mass of the system of particles shown in figure.

उत्तर
From the figure, the velocities of different masses can be written as:
\[\text{For m}_1 = 1 . 0 \text{kg}, \]
\[\text{ Velocity, } \vec{v}_1 = \left( - 1 . 5 \cos 37^\circ \hat i - 1.5 \sin 37^\circ\hat j\right) = - 1 . 2 \hat i- 0.9 \hat j\]
\[\text{For m}_2 = 1 . 2 \text{kg}, \]
\[\text{Velocity}, \vec{v}_2 = 0 . 4 \vec{j} \]
\[\text{For m}_3 = 1 . 5 \text{kg,} \]
\[\text{Velocity,} \vec{v}_3 = - 1 . 0 \cos 37^\circ \hat i0 + 1.0 \sin 37^\circ\hat j \]
\[\text{ For m}_4 = 0 . 50 \text{kg}, \]
\[\text{ Velocity,} \vec{v}_4 = 3 . 0 \hat i \]
\[\text{ For m}_5 = 1 . 0 \text{ kg}, \]
\[\text{ Velocity }, \vec{v}_5 = 2 . 0 \cos 37^\circ \hat i - 2 . 0 \sin 37^\circ \hat j \]
\[(\cos 37^\circ = \frac{4}{5} \text{ and } \sin 37^\circ \ = \frac{3}{5})\]
\[ V_{cm} = \frac{m_1 \vec{v}_1 + m_2 \vec{v}_2 + m_3 \vec{v}_3 + m_4 \vec{v}_4 + m_5 \vec{v}_5}{m_1 + m_2 + m_3 + m_4 + m_5}\]
\[ = \frac{1}{1 . 0 + 1 . 2 + 1 . 5 + 1 . 0 + 0 . 50}^\left[ 1 . 0\left( - 1 . 5 \times \frac{4}{5} \vec{i} - 1 . 5 \times \frac{3}{5} \vec{j} \right) + . . . - 2 . 0 \times \frac{3}{5} \vec{j} \right] \]
On solving the above equation, we get:
Vcm is 0.20 m/s , at 45° below the direction, towards right.
APPEARS IN
संबंधित प्रश्न
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
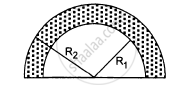
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
In rotational motion of a rigid body, all particles move with ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
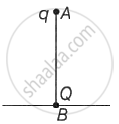
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.