Advertisements
Advertisements
प्रश्न
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
उत्तर
It is given that:
Mass of Mr. Verma, m1 = 50 kg
Mass of Mr. Mathur, m2 = 60 kg
Mass of boat, m3 = 40 kg
Let A be the origin of the system (boat plus two men).
Initially, Mr. Verma and Mr. Mathur were at two extremes of the boat.
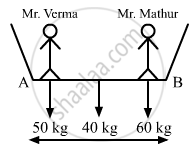
∴ Distance of the centre of mass:
\[X_{cm} = \frac{m_1 \times x_1 + m_2 \times x_2 + m_3 \times x_3}{m_1 + m_2 + m_3}\]
\[ = \frac{60 \times 0 + 50 \times 4 + 40 \times 2}{60 + 50 + 40}\]
\[ = \frac{280}{150} = 1 . 87 \text{ m from A}\]
As no external force is experienced in longitudinal direction, the centre of mass would not shift.
Initially, the centre of mass lies at a distance of 2 m from A.
When the men move towards the middle of the boat, the centre of mass shifts and lies at 1.87 m from A.
Therefore, the shift in centre of mass = 2 − 1.87 = 0.13 m, towards right
Hence, the boat moves 13 cm or 0.13 m towards right.
APPEARS IN
संबंधित प्रश्न
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 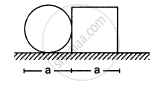
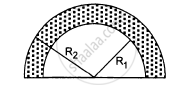
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
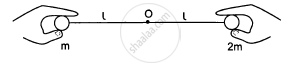
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
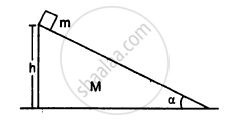
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
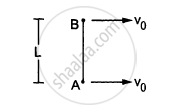
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
[Hint : The light rod will exert a force on the ball B
only along its length.]
The centre of mass of a system of particles does not depend upon, ______
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
