Advertisements
Advertisements
प्रश्न
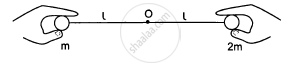
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
उत्तर
Given:
Mass of the 1st ball = m
Mass of the 2nd ball = 2m
When the balls reach the lower end,
Let the velocity of m be v; and the velocity of 2m be v'.
Using the work-energy theorem, we can write:
\[\left( \frac{1}{2} \right) \times m v^2 - \left( \frac{1}{2} \right) \times m(0 )^2 = mgl\]
\[ \Rightarrow v = \sqrt{2gl}\]
\[\text{ Similarly, velocity of block having mass 2m will be, }\]
\[v' = \sqrt{2gl}\]
\[\therefore v = v' = u (say)\]
Let the velocities of m and 2m after the collision be v1 and v2 respectively.
Using the law of conservation of momentum, we can write:
\[m \times u - 2mu = m v_1 + 2m v_2 \]
\[ \Rightarrow v_1 + 2 v_2 = - u . . . (1)\]
\[\text{ On applying collision formula, we get: }\]
\[ v_1 - v_2 = [(u - v)] = - 2u . . . (2)\]
\[\text{ Substracting equation } \left( 1 \right) \text{ from } \left( 2 \right), \text{ we get: } \]
\[3 v_2 = u\]
\[ \Rightarrow v_2 = \frac{u}{3} = \sqrt{\frac{2gl}{3}}\]
\[\text{ Substituting this value in equation (1), we get: }\]
\[ v_1 - v_2 = - 2u\]
\[ \Rightarrow v_1 = - 2u + v_2 \]
\[ = - 2u + \left( \frac{u}{3} \right)\]
\[ = \frac{- 5}{3}u = \frac{- 5}{3} \times \sqrt{2gl}\]
\[ = \frac{- \sqrt{50gl}}{3}\]
(b) Let the heights reached by balls 2m and m be h1 and h respectively.
Using the work energy principle, we get:
\[\left( \frac{1}{2} \right) \times 2m \times (0 )^2 - \left( \frac{1}{2} \right) \times 2m \times \left( v_2 \right)^2 = - 2m \times g \times h_1 \]
\[ \Rightarrow h_1 = \left( \frac{l}{9} \right)\]
\[\text{ Similarly,} \]
\[\left( \frac{1}{2} \right) \times m \times (0 )^2 - \left( \frac{1}{2} \right) \times m v_1^2 = m \times g \times h_2 \]
\[ \Rightarrow \left( \frac{1}{2} \right) \times \frac{50gl}{9} = g \times h_2 \]
\[ \Rightarrow h_2 = \frac{25l}{9}\]
As h2 is more than 2l, the velocity at the highest point will not be zero.
Also, the mass m will rise by a distance 2l.
APPEARS IN
संबंधित प्रश्न
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
Calculate the velocity of the centre of mass of the system of particles shown in figure.

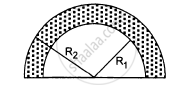
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Centre of mass is a point ______.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
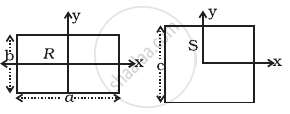
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
