Advertisements
Advertisements
प्रश्न
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
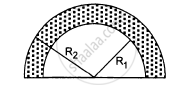
उत्तर
Let the mass of the plate be M.
Consider a small semicircular portion of mass dm and radius r, as shown in fig. 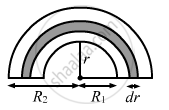
\[\text{dm} = \frac{M\pi rdr}{\frac{\pi\left( R_2^2 - R_1^2 \right)}{2}} = \frac{M}{\frac{\left( R_2^2 - R_1^2 \right)}{2}}\text{rdr}\]
The centre of mass is given as:
\[y_{cm} = \frac{\int y \text{dm}}{M}\]
\[y_{cm} = \int_{R_1}^{R_2} \left( \frac{2r}{\pi} \right) . \frac{M}{\frac{\left( R_2^2 - R_1^2 \right)}{2}} \times \frac{\text{rdr}}{M}\]
\[ = \frac{2}{\pi\frac{\left( R_2^2 - R_1^2 \right)}{2}} \int_{R_1}^{R_2} r^2 dr\]
\[ = \frac{2}{\pi\frac{\left( R_2^2 - R_1^2 \right)}{2}}\left[ \frac{\left( R_2^3 - R_1^3 \right)}{3} \right]\]
\[ = \frac{4\left( R_1^2 + R_1 R_2 + R_2^2 \right)}{3\pi\left( R_1 + R_2 \right)}\]
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 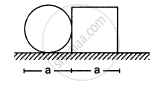
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
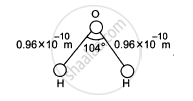
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Calculate the velocity of the centre of mass of the system of particles shown in figure.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
In an elastic collision
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
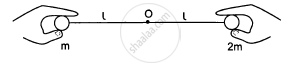
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Define centre of mass.
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
The centre of mass of a system of two particles divides the distance between them ______.
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
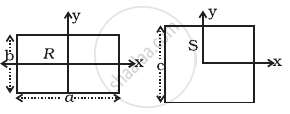
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
