Advertisements
Advertisements
प्रश्न
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
उत्तर
Given:
Initial velocity of the projectile = u
Angle of projection of the projectile with respect to ground = θ
When the projectile hits the ground for the first time, the velocity remains same i.e. u.
The component of velocity parallel to ground, u cos θ should remain constant.
However, the vertical component of the projectile undergoes a change after the collision.
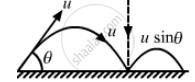
If the coefficient of restitution of collision between the projectile and the field is e,
The velocity of separation is given by,
⇒ v = eu sin θ
Therefore, for the second projectile motion,
Velocity of projection (u') will be,
\[u' = \sqrt{(u \cos \theta )^2 + (eu \sin \theta )^2}\]
\[\text{ Angle of projection,} \alpha = \tan^{- 1} \left( \frac{eu \sin \theta}{u \cos \theta} \right)\]
\[ \Rightarrow \alpha = \tan^{- 1} (e \tan \theta)\]
\[\text{or}, \tan \alpha = e \tan \theta . . . (2)\]
\[\text{Also, y} = x \tan \alpha - \left( \frac{g x^2 \sec^2 \alpha}{2u '^2} \right) . . . (3)\]
\[\text{Here, y} = 0 \]
\[ \therefore \tan \alpha = e \tan \theta\]
\[ \Rightarrow \sec^2 \alpha = 1 + e^2 \tan^2 \theta\]
\[\text{and }u '^2 = u^2 \cos^2 \theta + e^2 u^2 \sin^2 \theta\]
Putting the above calculated values in equation (3), we get:
\[\text{xe } tan\theta = \frac{g x^2 (1 + e^2 \tan^2 \theta)}{2 u^2 ( \cos^2 \theta + e^2 \sin^2 \theta)}\]
\[\text{ or, x } = \frac{2e u^2 \tan \theta ( \cos^2 \theta + e^2 \sin^2 \theta)}{g(1 + e^2 \tan^2 \theta)}\]
\[ \Rightarrow x = \frac{2e u^2 \tan \theta . \cos^2 \theta}{g}\]
\[ \Rightarrow x = \frac{e u^2 \sin 2\theta}{g}\]
Thus, from the starting point the projectile makes its second collision with the field at a distance,
\[x' = \frac{u^2 \sin 2\theta}{g} + \frac{e u^2 \sin 2\theta}{g}\]
\[ \Rightarrow x' = \frac{u^2 \sin 2\theta}{g}(1 + e)\]
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
In an elastic collision
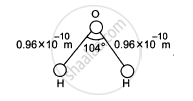
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
Calculate the velocity of the centre of mass of the system of particles shown in figure.

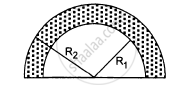
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
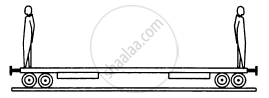
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
The centre of mass of a system of particles does not depend upon, ______
Which of the following points is the likely position of the centre of mass of the system shown in figure?
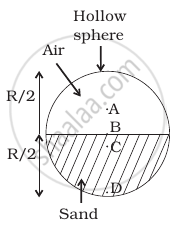
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
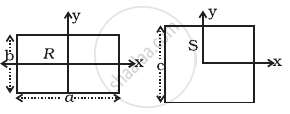
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
