Advertisements
Advertisements
प्रश्न
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
उत्तर
Given:
Initial velocity of the projectile = u
Angle of projection of the projectile with respect to ground = θ
When the projectile hits the ground for the first time, the velocity remains same i.e. u.
The component of velocity parallel to ground, u cos θ should remain constant.
However, the vertical component of the projectile undergoes a change after the collision.
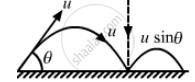
If the coefficient of restitution of collision between the projectile and the field is e,
The velocity of separation is given by,
⇒ v = eu sin θ
Therefore, for the second projectile motion,
Velocity of projection (u') will be,
\[u' = \sqrt{(u \cos \theta )^2 + (eu \sin \theta )^2}\]
\[\text{ Angle of projection,} \alpha = \tan^{- 1} \left( \frac{eu \sin \theta}{u \cos \theta} \right)\]
\[ \Rightarrow \alpha = \tan^{- 1} (e \tan \theta)\]
\[\text{or}, \tan \alpha = e \tan \theta . . . (2)\]
\[\text{Also, y} = x \tan \alpha - \left( \frac{g x^2 \sec^2 \alpha}{2u '^2} \right) . . . (3)\]
\[\text{Here, y} = 0 \]
\[ \therefore \tan \alpha = e \tan \theta\]
\[ \Rightarrow \sec^2 \alpha = 1 + e^2 \tan^2 \theta\]
\[\text{and }u '^2 = u^2 \cos^2 \theta + e^2 u^2 \sin^2 \theta\]
Putting the above calculated values in equation (3), we get:
\[\text{xe } tan\theta = \frac{g x^2 (1 + e^2 \tan^2 \theta)}{2 u^2 ( \cos^2 \theta + e^2 \sin^2 \theta)}\]
\[\text{ or, x } = \frac{2e u^2 \tan \theta ( \cos^2 \theta + e^2 \sin^2 \theta)}{g(1 + e^2 \tan^2 \theta)}\]
\[ \Rightarrow x = \frac{2e u^2 \tan \theta . \cos^2 \theta}{g}\]
\[ \Rightarrow x = \frac{e u^2 \sin 2\theta}{g}\]
Thus, from the starting point the projectile makes its second collision with the field at a distance,
\[x' = \frac{u^2 \sin 2\theta}{g} + \frac{e u^2 \sin 2\theta}{g}\]
\[ \Rightarrow x' = \frac{u^2 \sin 2\theta}{g}(1 + e)\]
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
In an elastic collision
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.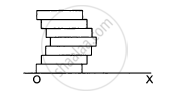
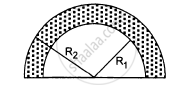
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
In an elastic collision
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
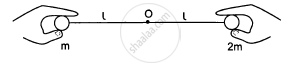
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
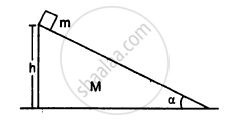
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Define centre of mass.
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
