Advertisements
Advertisements
Question
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Solution
Given:
Initial velocity of the projectile = u
Angle of projection of the projectile with respect to ground = θ
When the projectile hits the ground for the first time, the velocity remains same i.e. u.
The component of velocity parallel to ground, u cos θ should remain constant.
However, the vertical component of the projectile undergoes a change after the collision.
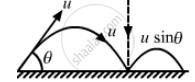
If the coefficient of restitution of collision between the projectile and the field is e,
The velocity of separation is given by,
⇒ v = eu sin θ
Therefore, for the second projectile motion,
Velocity of projection (u') will be,
\[u' = \sqrt{(u \cos \theta )^2 + (eu \sin \theta )^2}\]
\[\text{ Angle of projection,} \alpha = \tan^{- 1} \left( \frac{eu \sin \theta}{u \cos \theta} \right)\]
\[ \Rightarrow \alpha = \tan^{- 1} (e \tan \theta)\]
\[\text{or}, \tan \alpha = e \tan \theta . . . (2)\]
\[\text{Also, y} = x \tan \alpha - \left( \frac{g x^2 \sec^2 \alpha}{2u '^2} \right) . . . (3)\]
\[\text{Here, y} = 0 \]
\[ \therefore \tan \alpha = e \tan \theta\]
\[ \Rightarrow \sec^2 \alpha = 1 + e^2 \tan^2 \theta\]
\[\text{and }u '^2 = u^2 \cos^2 \theta + e^2 u^2 \sin^2 \theta\]
Putting the above calculated values in equation (3), we get:
\[\text{xe } tan\theta = \frac{g x^2 (1 + e^2 \tan^2 \theta)}{2 u^2 ( \cos^2 \theta + e^2 \sin^2 \theta)}\]
\[\text{ or, x } = \frac{2e u^2 \tan \theta ( \cos^2 \theta + e^2 \sin^2 \theta)}{g(1 + e^2 \tan^2 \theta)}\]
\[ \Rightarrow x = \frac{2e u^2 \tan \theta . \cos^2 \theta}{g}\]
\[ \Rightarrow x = \frac{e u^2 \sin 2\theta}{g}\]
Thus, from the starting point the projectile makes its second collision with the field at a distance,
\[x' = \frac{u^2 \sin 2\theta}{g} + \frac{e u^2 \sin 2\theta}{g}\]
\[ \Rightarrow x' = \frac{u^2 \sin 2\theta}{g}(1 + e)\]
APPEARS IN
RELATED QUESTIONS
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 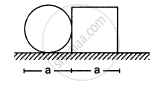
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.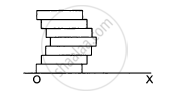
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
In an elastic collision
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
Solve the following problem.
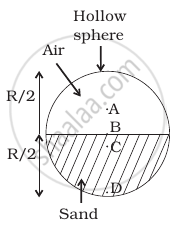
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
A mass of 1kg is suspended by a string. It is first lifted up with an acceleration of 4.9 m/s2 and then lowered down with same acceleration. The ratio of tensions in the string in the two cases, respectively is g = 9.8 m/s2 ______.
In rotational motion of a rigid body, all particles move with ______.
Which of the following points is the likely position of the centre of mass of the system shown in figure?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
