Advertisements
Advertisements
Question
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.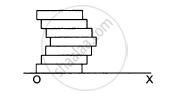
Solution
Let OX be the X-axis and point O (0, 0) be the origin of the system.
The mass of each brick is M.
The length of each brick is L.
Each brick is displaced with respect to another in contact by a distance \[\frac{L}{10}\] .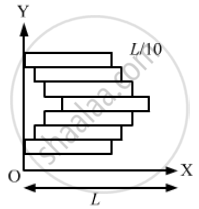
∴ The X-coordinate of the centre of mass is given as,
\[X_{cm} = \frac{1}{7 m\frac{L}{10}}^\left\{ \frac{mL}{2} + m\left( \frac{L}{2} + \frac{L}{10} \right) + . . . . . . . . . . + m\left( \frac{L}{2} \right) \right\} \]
\[ X_{cm} = \frac{\frac{L}{2} + \frac{L}{2} + \frac{L}{10} + \frac{L}{5} + \frac{L}{2} + \frac{3L}{10} + \frac{L}{2} + \frac{L}{5} + \frac{L}{2} + \frac{L}{10} + \frac{L}{2}}{7}\]
\[ = \frac{7\frac{L}{2} + 5\frac{L}{10} + 2\frac{L}{5}}{7} = \frac{22L}{35}\]
The X-coordinate of the centre of mass relative to the origin is \[\frac{22L}{35}\]
APPEARS IN
RELATED QUESTIONS
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
You are waiting for a train on a railway platform. Your three-year-old niece is standing on your iron trunk containing the luggage. Why does the trunk not recoil as she jumps off on the platform?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 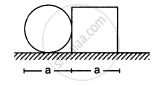
In an elastic collision
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.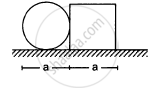
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
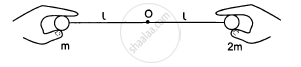
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
For which of the following does the centre of mass lie outside the body?
Which of the following points is the likely position of the centre of mass of the system shown in figure?
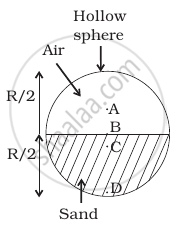
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
