Advertisements
Advertisements
Question
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
Solution
Given,
Mass of the man, Mm = 50 kg
Mass of the pillow, MP = 5 kg
Velocity of pillow w.r.t. man, \[\vec{V}_{pm}\]= 8 ft/s
Let the velocity of man be \[\vec{V}_m\] .
\[\vec{V}_{pm} = \vec{V}_p - ( - \vec{V}_m )\]
\[ = \vec{V}_p + \vec{V}_m \]
\[ \Rightarrow \vec{V}_p = \vec{V}_{pm} - \vec{V}_m\]
As no external force acts on the system, the acceleration of centre of mass is zero and the velocity of centre of mass remains constant.
Using the law of conservation of linear momentum:
Mm × Vm = Mp × Vp ...(1)
\[M_m \times V_m = M_p \times ( V_{pm} - V_m )\]
\[ \Rightarrow 50 \times V_m = 5 \times (8 - V_m )\]
\[ \Rightarrow V_m = \frac{8}{11} = 0 . 727 \text{ ft/s }\]
∴ Velocity of pillow, \[\vec{V}_p\] = 8 − 0.727 = 7.2 ft/s
The time taken to reach the floor is given by,
\[t = \frac{s}{v} = \frac{8}{7 . 2} = 1 . 1 \text{ s}\]
As the mass of wall is much greater than the mass of the pillow,
velocity of block before the collision = velocity after the collision
⇒ time of ascent = 1.11 s
Hence, total time taken = 1.11 + 1.11 = 2.22 s
APPEARS IN
RELATED QUESTIONS
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
The centre of mass of a system of particles is at the origin. It follows that
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
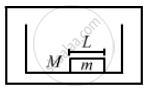
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
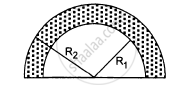
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
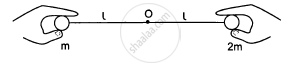
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of two particles divides the distance between them ______.
Which of the following has maximum momentum?
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Which of the following points is the likely position of the centre of mass of the system shown in figure?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
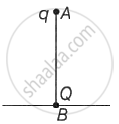
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.