Advertisements
Advertisements
प्रश्न
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
उत्तर
Given,
Mass of the man, Mm = 50 kg
Mass of the pillow, MP = 5 kg
Velocity of pillow w.r.t. man, \[\vec{V}_{pm}\]= 8 ft/s
Let the velocity of man be \[\vec{V}_m\] .
\[\vec{V}_{pm} = \vec{V}_p - ( - \vec{V}_m )\]
\[ = \vec{V}_p + \vec{V}_m \]
\[ \Rightarrow \vec{V}_p = \vec{V}_{pm} - \vec{V}_m\]
As no external force acts on the system, the acceleration of centre of mass is zero and the velocity of centre of mass remains constant.
Using the law of conservation of linear momentum:
Mm × Vm = Mp × Vp ...(1)
\[M_m \times V_m = M_p \times ( V_{pm} - V_m )\]
\[ \Rightarrow 50 \times V_m = 5 \times (8 - V_m )\]
\[ \Rightarrow V_m = \frac{8}{11} = 0 . 727 \text{ ft/s }\]
∴ Velocity of pillow, \[\vec{V}_p\] = 8 − 0.727 = 7.2 ft/s
The time taken to reach the floor is given by,
\[t = \frac{s}{v} = \frac{8}{7 . 2} = 1 . 1 \text{ s}\]
As the mass of wall is much greater than the mass of the pillow,
velocity of block before the collision = velocity after the collision
⇒ time of ascent = 1.11 s
Hence, total time taken = 1.11 + 1.11 = 2.22 s
APPEARS IN
संबंधित प्रश्न
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
The centre of mass of a system of particles is at the origin. It follows that
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
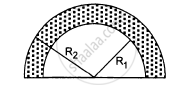
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
Which of the following has maximum momentum?
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
Which of the following statements are correct?
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
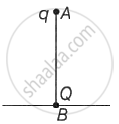
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.