Advertisements
Advertisements
प्रश्न
Consider a gravity-free hall in which an experimenter of mass 50 kg is resting on a 5 kg pillow, 8 ft above the floor of the hall. He pushes the pillow down so that it starts falling at a speed of 8 ft/s. The pillow makes a perfectly elastic collision with the floor, rebounds and reaches the experimenter's head. Find the time elapsed in the process.
उत्तर
Given,
Mass of the man, Mm = 50 kg
Mass of the pillow, MP = 5 kg
Velocity of pillow w.r.t. man, \[\vec{V}_{pm}\]= 8 ft/s
Let the velocity of man be \[\vec{V}_m\] .
\[\vec{V}_{pm} = \vec{V}_p - ( - \vec{V}_m )\]
\[ = \vec{V}_p + \vec{V}_m \]
\[ \Rightarrow \vec{V}_p = \vec{V}_{pm} - \vec{V}_m\]
As no external force acts on the system, the acceleration of centre of mass is zero and the velocity of centre of mass remains constant.
Using the law of conservation of linear momentum:
Mm × Vm = Mp × Vp ...(1)
\[M_m \times V_m = M_p \times ( V_{pm} - V_m )\]
\[ \Rightarrow 50 \times V_m = 5 \times (8 - V_m )\]
\[ \Rightarrow V_m = \frac{8}{11} = 0 . 727 \text{ ft/s }\]
∴ Velocity of pillow, \[\vec{V}_p\] = 8 − 0.727 = 7.2 ft/s
The time taken to reach the floor is given by,
\[t = \frac{s}{v} = \frac{8}{7 . 2} = 1 . 1 \text{ s}\]
As the mass of wall is much greater than the mass of the pillow,
velocity of block before the collision = velocity after the collision
⇒ time of ascent = 1.11 s
Hence, total time taken = 1.11 + 1.11 = 2.22 s
APPEARS IN
संबंधित प्रश्न
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.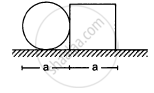
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
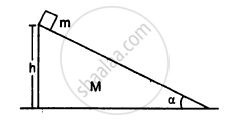
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system.
Define centre of mass.
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The centre of mass of a system of two particles divides the distance between them ______.
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
The mass per unit length of a non-uniform rod of length L varies as m = λx where λ is constant. The centre of mass of the rod will be at ______.
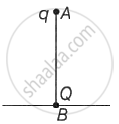
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.