Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
उत्तर
Given:
Force on block of mass, m1 = F1
Force on block of mass, m2 = F2
Let the acceleration produced in mass m1 be a1.
\[a_1 = \frac{F_1 - F_2}{m_1 + m_2}\]
Let the acceleration of mass m2 be a2.
\[a_2 = \frac{F_2 - F_1}{m_1 + m_2}\]
Due to the force F2, the mass m1 experiences a pseudo force.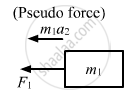
\[\therefore \text{ Net force on m}_1 = F_1 + m_1 a_2 \]
\[F' = F_1 + m_1 \times \frac{( F_2 - F_1 )}{m_1 + m_2}\]
\[ = \frac{m_1 F_1 + m_2 F_1 + m_1 F_2 - m_1 F_1}{m_1 + m_2}\]
\[ = \frac{m_2 F_1 + m_1 F_2}{m_1 + m_2}\]
Similarly, mass m2 experiences a pseudo force due to force F1.
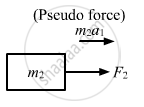
\[\therefore \text{ Net force on m}_2 = F_2 + m_2 a_1\]
\[F " = F_2 + m_2 \times \frac{( F_1 - F_2 )}{m_1 + m_2}\]
\[ = \frac{m_1 F_2 + m_2 F_2 + m_2 F_1 - m_2 F_2}{m_1 + m_2}\]
\[ = \frac{m_1 F_2 + m_2 F_1}{m_1 + m_2}\]
Let m1 be displaced by a distance x1 and m2 be displaced by a distance x2.
Therefore, the maximum elongation of the spring = x1 + x2
Work done by the blocks = Energy stored in the spring
\[\Rightarrow \frac{m_2 F_1 + m_1 F_2}{m_1 + m_2} \times x_1 \times \frac{m_2 F_1 + m_1 F_2}{m_1 + m_2} \times x_2 = \left( \frac{1}{2} \right)k( x_1 + x_2 )^2 \]
\[ \Rightarrow x_1 + x_2 = \frac{2}{k}\left( \frac{m_1 F_2 + m_2 F_1}{m_1 + m_2} \right)\]
APPEARS IN
संबंधित प्रश्न
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 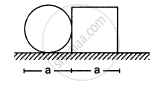
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
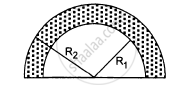
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1 and R2.
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
Which of the following statements are correct?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
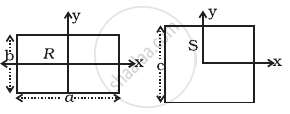
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
The spheres of masses 2 kg and 4 kg are situated at the opposite ends of wooden bars of length 9 m. Where does the centre of mass of the system will ______.
