Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
उत्तर
It is given that the force on both the blocks is F.
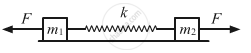
Let x1 and x2 be the extensions of blocks m1 and m2 respectively.
Total work done by the forces on the blocks = Fx1 + Fx2 ...(1)
∴ Increase in the potential energy of spring = \[\left( \frac{1}{2} \right)K( x_1 + x_2 )^2 . . . (2)\]
\[\text{ Equating the equations (1) and (2), we get: } \]
\[ \Rightarrow ( x_1 + x_2 ) = \left( \frac{2F}{k} \right) \ldots(3)\]
As the net external force on the system is zero, the centre of mass does not shift.
\[\therefore m_1 x_1 = m_2 x_2 . . . (4)\]
\[\text{ Using the equations }\left( 3 \right) \text{ and } \left( 4 \right), \text{ we get}: \]
\[ \frac{m_1}{m_2} x_1 + x_1 = \frac{2F}{k}\]
\[ \Rightarrow x_1 \left( 1 + \frac{m_1}{m_2} \right) = \frac{2F}{k}\]
\[ \Rightarrow x_1 = \frac{2F m_2}{k( m_1 + m_2 )}\]
Similarly,
\[x_2 = \frac{2F m_1}{k( m_1 + m_2 )}\]
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 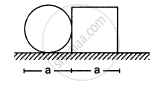
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.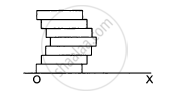
Calculate the velocity of the centre of mass of the system of particles shown in figure.

A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
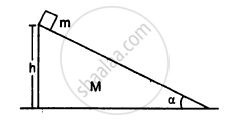
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
A shell of mass 'M' initially at rest suddenly explodes in three fragments. Two of these fragments are of mass 'M/4' each, which move with velocities 3 ms-1 and 4 ms-1 respectively in mutually perpendicular directions. The magnitude of velocity of the third fragment is ______.
In rotational motion of a rigid body, all particles move with ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
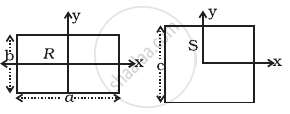
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
