Advertisements
Advertisements
प्रश्न
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
उत्तर
It is given that the mass of the ball is m.
Let the ball be dropped from a height h.
The speed of ball before the collision is v1.
\[\therefore \text{v}_1 = \sqrt{2\text{gh}}\]
The speed of ball after the collision is v2.
\[\text{v}_2 = - \sqrt{2\text{gh}}\]
\[\text{ Rate of change of velocity = acceleration }\]
\[ \Rightarrow a = \frac{2\sqrt{2gh}}{t}\]
\[ \therefore \text{ Force}, F = \frac{m \times 2\sqrt{2gh}}{t} \ldots(1)\]
Using Newton's laws of motion, we can write:
\[v = \sqrt{2gh}, s = h, u = 0\]
\[ \Rightarrow \sqrt{2gh} = gt\]
\[\Rightarrow t = \sqrt{\frac{2h}{g}}\]
\[ \therefore \text{ Total time }= 2\sqrt{\frac{2h}{g}}\]
Substituting this value of time t in equation (1), we get:
F = mg
APPEARS IN
संबंधित प्रश्न
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
Consider the following two statements:
(A) Linear momentum of the system remains constant.
(B) Centre of mass of the system remains at rest.
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
In an elastic collision
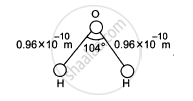
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
A square plate of edge d and a circular disc of diameter d are placed touching each other at the midpoint of an edge of the plate as shown in figure. Locate the centre of mass of the combination, assuming same mass per unit area for the two plates.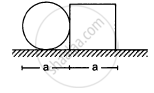
Calculate the velocity of the centre of mass of the system of particles shown in figure.

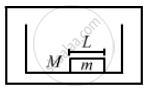
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
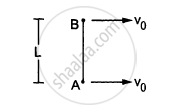
[Hint : The light rod will exert a force on the ball B
only along its length.]
Find out the centre of mass for the given geometrical structures.
a) Equilateral triangle
b) Cylinder
c) Square
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
Three equal masses each of 50 g, are placed at the corners of a right angled isosceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is ____________.
A bullet of mass 20 gram is fired from a gun of mass 2.5 kg with a speed of 750 m/s. The magnitude of recoil velocity of the gun is ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Which of the following statements are correct?
