Advertisements
Advertisements
प्रश्न
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
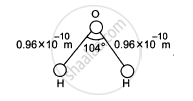
उत्तर
Let OX be the x-axis, OY be the Y-axis and O be the origin. 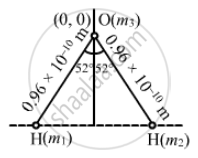
\[\text{ Mass of O atom, m}_1 = 16 \text{unit }\]
Let the position of oxygen atom be origin.
\[\Rightarrow x_1 = y_1 = 0\]
\[\text{ Mass of H atom ,m}_2 = 1 \text{unit}\]
\[ x_2 = - 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_2 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ\]
\[\text{Now, m}_3 = 1 \text{unit}\]
\[ x_3 = 0 . 96 \times {10}^{- 10} \sin 52^\circ\]
\[ y_3 = - 0 . 96 \times {10}^{- 10} \cos 52^\circ \]
The X coordinate of the center of mass is given by:
\[ x_{cm} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 1 \times \left( - 0 . 96 \times {10}^{- 10} \sin 52^\circ\right) + 1 \times 0 . 96 \times {{10}^-}^{10} \sin 52^\circ] }{1 + 1 + 16} = 0\]
\[\text{ The Y coordinate of the center of mass is given by: }\]
\[ y_{cm} = \frac{m_1 y_1 + m_2 y_2 + m_3 y_3}{m_1 + m_2 + m_3}\]
\[ = \frac{16 \times 0 + 2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{1 + 1 + 16}\]
\[ = \frac{2 \times 0 . 96 \times {10}^{- 10} \cos 52^\circ]}{18}\]
\[ = 6 . 4 \times {10}^{- 12} \text{m}\]
Hence, the distance of centre of mass of the molecule from the centre of the oxygen atom is (\[ = 6 . 4 \times {10}^{- 12} \text{m}\]).
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
The speed of the centre of a wheel rolling on a horizontal surface is vo. A point on the rim is level with the centre will be moving at a speed of, ______
A body of mass 2 kg is acted upon by two forces each of magnitude 1 N and inclined at 60° with each other. The acceleration of the body in m/s is ____________. [cos 60° = 0.5]
A mass of 1kg is suspended by a string. It is first lifted up with an acceleration of 4.9 m/s2 and then lowered down with same acceleration. The ratio of tensions in the string in the two cases, respectively is g = 9.8 m/s2 ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
For which of the following does the centre of mass lie outside the body?
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
