Advertisements
Advertisements
प्रश्न
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
उत्तर
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
As the density continuously increases/decreases from left to right, there will be difference in the masses of rod that lie on either sides of the centre of mass. Thus, the centre of mass of a rod in such a case will certainly not be at its centre.
APPEARS IN
संबंधित प्रश्न
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
In an elastic collision
If the external force acting on a system have zero resultant, the centre of mass
(a) must not move
(b) must not accelerate
(c) may move
(d) may accelerate.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.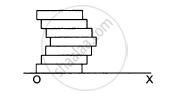
Calculate the velocity of the centre of mass of the system of particles shown in figure.

Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raise the centre of mass by 1 cm?
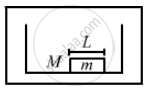
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
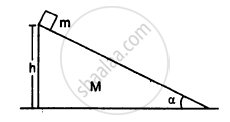
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
In rotational motion of a rigid body, all particles move with ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
