Advertisements
Advertisements
प्रश्न
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
उत्तर
(a) Take a system of i moving particles.
Mass of the ith particle = mi
Velocity of the ith particle = vi
Hence, momentum of the ith particle, pi = mi vi
Velocity of the centre of mass = V
The velocity of the ith particle with respect to the centre of mass of the system is given as:
v’i = vi – V … (1)
Multiplying mi throughout equation (1), we get:
mi v’i = mi vi – mi V
p’i = pi – mi V
Where,
pi’ = mivi’ = Momentum of the ith particle with respect to the centre of mass of the system
∴pi = p’i + mi V
We have the relation: p’i = mivi’
Taking the summation of the momentum of all the particles with respect to the centre of mass of the system, we get:
`sum_("i") "p"_"t" = sum_("i")"m"
_"iv"_"t" = sum_("i")"m"_"i" ("dr"_"t")/"dt"`
Where
`"r""'"_"t" `= Position vector of the ith particle with respect to the centre of mass
`"v"_"t" = ("dr"_"t")/"dt"`
As per the definition of the centre of mass, we have
`sum_("i") "m"_"ir"_"t" = 0`
`:. sum_("i") "m"_"i" ("dr"_"t")/"dt" = 0`
`sum_("i") "p"_"i" = 0`
(b) We have the relation for the velocity of the ith particle as:
vi = v’i + V
`sum_("i")"m"_"i" "v"_"i" = sum_("i") "m"_"i" "v"_"t" + sum_("i")"m"_"i" "V"` ....(2)
Taking the dot product of equation (2) with itself, we get:
`sum_("i")"m"_"i" "v"_"i" .sum_("i") "m"_"iv"_"i" = sum_("i") "m"_"i"("v"_"i" + "V").sum_("i") "m"_"i"("v"_"i" + "V")`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i") "v"_"i"^2 + "M"^2 sum_("i") "v"_"i". "v"_"i"+ "M"^2 sum_("i") "v"_"i"."v"_"i" + "M"^2"V"^2`
Here, for the centre of mass of the system of particle
`sum_("i")"v"_"i"."v"_"i" =-sum_("i")"v"_"i"."v"_"i"`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i")"v"^2_"i" + "M"^2"V"^2`
`1/2 "M" sum_("i") "v"_"i"^('2) = 1/2 "M" sum_("i") "v"_"i"^('2) + 1.2 "MV"^2 `
`"K" = "K" + 1/2 "MV"^2`
Where
`"K" = 1/2 "M"sum_("i")"v"_"i"
^2` = Total kinetic energy of the system of particles
`"K""'" = 1/2 "M" sum_("i")"v"_"i"^(2)` = Total kinetic energy of the system of particles with respect to the centre of mass
`1/2 "MV"^2` = Kinetic energy of the translation of the system as a whole.
(c) Position vector of the ith particle with respect to origin = ri
Position vector of the ith particle with respect to the centre of mass = r’i
Position vector of the centre of mass with respect to the origin = R
It is given that:
r’i = ri – R
ri = r’i + R
We have from part (a),
pi = p’i + mi V
Taking the cross product of this relation by ri, we get:
`sum_("i")"r"_"i" xx "p"_"i" = sum_("i")"r"_"i"xx"p""'"_"i" + sum_("i") "r"_"i" xx "m"_"i" "V"`
`"L" = sum_("i") ("r""'"_"i" + "R" )xx "p""'"_"i" + sum_("i")("r""'"_"i" + "R") xx "m"_"iV"`
`= sum_("i")"r""'"_"i" xx "p""'"_"i" + sum_("i") ("r""'"_"i"+ "R") xx "m"_"iV"`
`= "L""'" + sum_("i") + sum_("i")"R" xx "p""'"_"i" + sum_("i") "r""'"_"i" xx "m"_"iV"+ sum_("i")"R" xx "m"_"iV"`
Where
`"R" xx sum_("i") "p""'"_"i" = 0` and `(sum_("i")"r""'"_"i") xx "MV" = 0`
`sum_("i") "m"_"i" = "M"`
`:."L" = "L""'" + "R" xx "MV"`
(d) Show `("dL""'")/"dt" = sum "r'"_"t" xx ("dp""'")/"dt"`
Further, show that
`("dL'")/("dt") = tau"'"_"ext"`
where `tau"'"_"ext"` is the sum of all external torques acting on the system about the
centre of mass.
(Hint : Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)
APPEARS IN
संबंधित प्रश्न
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube,
each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
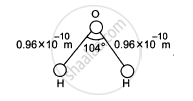
The structure of a water molecule is shown in figure. Find the distance of the centre of mass of the molecule from the centre of the oxygen atom.
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.
The radius and mass of earth are increased by 0.5%. Which of the following statements are true at the surface of the earth?
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind figure. The CM of the plate is now in the following quadrant of x-y plane ______.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
