Advertisements
Advertisements
Question
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
Solution
(a) Take a system of i moving particles.
Mass of the ith particle = mi
Velocity of the ith particle = vi
Hence, momentum of the ith particle, pi = mi vi
Velocity of the centre of mass = V
The velocity of the ith particle with respect to the centre of mass of the system is given as:
v’i = vi – V … (1)
Multiplying mi throughout equation (1), we get:
mi v’i = mi vi – mi V
p’i = pi – mi V
Where,
pi’ = mivi’ = Momentum of the ith particle with respect to the centre of mass of the system
∴pi = p’i + mi V
We have the relation: p’i = mivi’
Taking the summation of the momentum of all the particles with respect to the centre of mass of the system, we get:
`sum_("i") "p"_"t" = sum_("i")"m"
_"iv"_"t" = sum_("i")"m"_"i" ("dr"_"t")/"dt"`
Where
`"r""'"_"t" `= Position vector of the ith particle with respect to the centre of mass
`"v"_"t" = ("dr"_"t")/"dt"`
As per the definition of the centre of mass, we have
`sum_("i") "m"_"ir"_"t" = 0`
`:. sum_("i") "m"_"i" ("dr"_"t")/"dt" = 0`
`sum_("i") "p"_"i" = 0`
(b) We have the relation for the velocity of the ith particle as:
vi = v’i + V
`sum_("i")"m"_"i" "v"_"i" = sum_("i") "m"_"i" "v"_"t" + sum_("i")"m"_"i" "V"` ....(2)
Taking the dot product of equation (2) with itself, we get:
`sum_("i")"m"_"i" "v"_"i" .sum_("i") "m"_"iv"_"i" = sum_("i") "m"_"i"("v"_"i" + "V").sum_("i") "m"_"i"("v"_"i" + "V")`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i") "v"_"i"^2 + "M"^2 sum_("i") "v"_"i". "v"_"i"+ "M"^2 sum_("i") "v"_"i"."v"_"i" + "M"^2"V"^2`
Here, for the centre of mass of the system of particle
`sum_("i")"v"_"i"."v"_"i" =-sum_("i")"v"_"i"."v"_"i"`
`"M"^2sum_("i") "v"_"i"^2 = "M"^2 sum_("i")"v"^2_"i" + "M"^2"V"^2`
`1/2 "M" sum_("i") "v"_"i"^('2) = 1/2 "M" sum_("i") "v"_"i"^('2) + 1.2 "MV"^2 `
`"K" = "K" + 1/2 "MV"^2`
Where
`"K" = 1/2 "M"sum_("i")"v"_"i"
^2` = Total kinetic energy of the system of particles
`"K""'" = 1/2 "M" sum_("i")"v"_"i"^(2)` = Total kinetic energy of the system of particles with respect to the centre of mass
`1/2 "MV"^2` = Kinetic energy of the translation of the system as a whole.
(c) Position vector of the ith particle with respect to origin = ri
Position vector of the ith particle with respect to the centre of mass = r’i
Position vector of the centre of mass with respect to the origin = R
It is given that:
r’i = ri – R
ri = r’i + R
We have from part (a),
pi = p’i + mi V
Taking the cross product of this relation by ri, we get:
`sum_("i")"r"_"i" xx "p"_"i" = sum_("i")"r"_"i"xx"p""'"_"i" + sum_("i") "r"_"i" xx "m"_"i" "V"`
`"L" = sum_("i") ("r""'"_"i" + "R" )xx "p""'"_"i" + sum_("i")("r""'"_"i" + "R") xx "m"_"iV"`
`= sum_("i")"r""'"_"i" xx "p""'"_"i" + sum_("i") ("r""'"_"i"+ "R") xx "m"_"iV"`
`= "L""'" + sum_("i") + sum_("i")"R" xx "p""'"_"i" + sum_("i") "r""'"_"i" xx "m"_"iV"+ sum_("i")"R" xx "m"_"iV"`
Where
`"R" xx sum_("i") "p""'"_"i" = 0` and `(sum_("i")"r""'"_"i") xx "MV" = 0`
`sum_("i") "m"_"i" = "M"`
`:."L" = "L""'" + "R" xx "MV"`
(d) Show `("dL""'")/"dt" = sum "r'"_"t" xx ("dp""'")/"dt"`
Further, show that
`("dL'")/("dt") = tau"'"_"ext"`
where `tau"'"_"ext"` is the sum of all external torques acting on the system about the
centre of mass.
(Hint : Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)
APPEARS IN
RELATED QUESTIONS
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 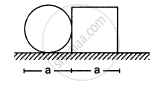
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
A car of mass M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes serval collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process.

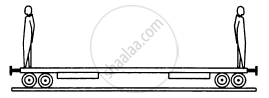
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
In rotational motion of a rigid body, all particles move with ______.
