Advertisements
Advertisements
Question
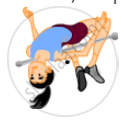
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
Solution
From the figure, it can be seen that when a high-jumper successfully clears the bar, it is possible that her centre of mass crosses the bar from below it because the legs as well as the arms of the high-jumper are below the bar.
Hence, the point shown in the figure can be her Centre of mass.
APPEARS IN
RELATED QUESTIONS
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
The centre of mass is defined as \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\]. Suppose we define "centre of charge" as \[\vec{R}_c = \frac{1}{Q} \sum_i q_i \vec{r_i}\] where qi represents the ith charge placed at \[\vec{r}_i\] and Q is the total charge of the system.
(a) Can the centre of charge of a two-charge system be outside the line segment joining the charges?
(b) If all the charges of a system are in X-Y plane, is it necessary that the centre of charge be in X-Y plane?
(c) If all the charges of a system lie in a cube, is it necessary that the centre of charge be in the cube?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
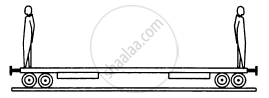
Two persons each of mass m are standing at the two extremes of a railroad car of mass M resting on a smooth track(In the following figure). The person on left jumps to the left with a horizontal speed u with respect to the state of the car before the jump. Thereafter, the other person jumps to the right, again with the same horizontal speed u with respect to the state of the car before his jump. Find the velocity of the car after both the persons have jumped off.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
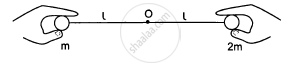
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The centre of mass of a system of two particles divides the distance between them ______.
Which of the following has maximum momentum?
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
For which of the following does the centre of mass lie outside the body?
