Advertisements
Advertisements
Question
During a heavy rain, hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10 m × 10 m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900 kg/m3.
Solution
It is given that:
Diameter of hailstone = 1 cm = 0.01 m
⇒ Radius of hailstone, r = 0.005 m
Average speed of hailstone = 20 m/s
Density of hailstone = 900 kg/m3 = 0.9 g/cm3
\[\text{ Volume of the hailstones is given as, }\]
\[V = \frac{4}{3}\pi r^3 \]
\[ \Rightarrow V = \frac{4}{3}\pi(0 . 005 )^3 = 5 . 235 \times {10}^{- 7} m^3 \]
\[\text{ Mass = volume }\times \text{ density } = 5 . 235 \times {10}^{- 7} \times 900\]
\[ = 4 . 711 \times {10}^{- 4} \text{ kg }\]
\[ \therefore \text{ Mass of 2000 hailstone } = 2000 \times 4 . 711 \times {10}^{- 4} = 0 . 9422\]
\[\text{ Rate of change of momentum } = 0 . 9422 \times 20 \approx 19 \text{N/ m}^2 \]
∴ The total force exerted on the roof = 19 × 100 = 1900 N
APPEARS IN
RELATED QUESTIONS
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.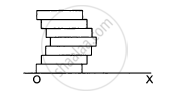
Calculate the velocity of the centre of mass of the system of particles shown in figure.

Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
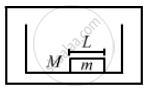
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
A block of mass 2.0 kg moving 2.0 m/s collides head on with another block of equal mass kept at rest. (a) Find the maximum possible loss in kinetic energy due to the collision. (b) If he actual loss in kinetic energy is half of this maximum, find the coefficient of restitution.
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
The axis of rotation of a purely rotating body
(a) must pass through the centre of mass
(b) may pass through the centre of mass
(c) must pass through a particle of the body
(d) may pass through a particle of the body.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
The centre of mass of a system of particles does not depend upon, ______
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Define centre of mass.
In rotational motion of a rigid body, all particles move with ______.
Figure shows a lamina in x-y plane. Two axes z and z ′ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to z′-axis than the z-axis.)

- Torque τ caused by F about z axis is along `-hatk`.
- Torque τ′ caused by F about z′ axis is along `-hatk`.
- Torque τ caused by F about z axis is greater in magnitude than that about z axis.
- Total torque is given be τ = τ + τ′.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.
