Advertisements
Advertisements
Question
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
Solution
It is given that:
Mass of particles = 100 g
Initial speed of the first particle = u
Final K.E. of the system after collision = 0.2J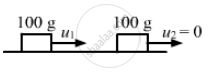
Initial K.E. of the system, before collision = \[\frac{1}{2}m u^2 + 0 \]
i.e. Initial K.E. = \[\frac{1}{2} \times 0 . 1 \times u^2 = 0 . 05 u^2\]
Let v1 and v2 be the final velocities of the first and second block respectively.
Let v1 and v2 be the final velocities of the first and second block respectively.
By law of conservation of momentum, we know:
\[m v_1 + m v_2 = mu\]
\[\Rightarrow v_1 + v_2 = u . . . (1)\]
\[( v_1 - v_2 ) + e( u_1 - u_2 ) = 0\]
\[ \Rightarrow eu = v_2 - v_1 . . . (2) [\text{ Putting } u_2 = 0, u_1 = u]\]
\[\text{ Adding the equations (1) and (2), we get:}\]
\[ 2 v_2 = (1 + e)u\]
\[ \Rightarrow v_2 = \left( \frac{u}{2} \right)(1 + e)\]
\[ \therefore v_1 = u - \frac{u}{2}(1 + e)\]
\[ v_1 = \frac{u}{2}(1 - e)\]
\[\text{ According to given condition, }\]
\[\frac{1}{2}m v_1^2 + \frac{1}{2}m v_2^2 = 0 . 2\]
\[ \Rightarrow v_1^2 + v_2^2 = 4\]
\[ \Rightarrow \frac{u^2}{2}\left( 1 + e^2 \right) = 4\]
\[ \Rightarrow u^2 = \frac{8}{1 + e^2}\]
For maximum value of u, denominator should be minimum in the above equation.
i.e. e = 0
⇒ u2 = 8
\[\Rightarrow u = 2\sqrt{2} \text{ m/s}\]
For minimum value of u, denominator should have maximum value.
i.e. e = 1
⇒ u2 = 4
⇒ u = 2 m/s .
APPEARS IN
RELATED QUESTIONS
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
In a head-on collision between two particles, is it necessary that the particles will acquire a common velocity at least for one instant?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
The centre of mass of a system of particles is at the origin. It follows that
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
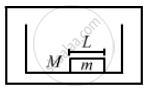
Consider a gravity-free hall in which a tray of mass M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle. If the ice melts, by what distance does the centre of mass of "the tray plus the ice" system descend?
Mr. Verma (50 kg) and Mr. Mathur (60 kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting friction with water, how far does the boat move on the water during the process?
Find the ratio of the linear momenta of two particles of masses 1.0 kg and 4.0 kg if their kinetic energies are equal.
Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from all other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will the spaceship move?
A railroad car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man approaching the engine?
A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point, does the projectile makes its second collision with the field?
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
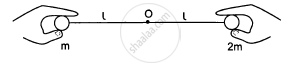
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
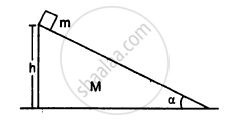
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
