Advertisements
Advertisements
Question
Two friends A and B (each weighing 40 kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4 kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5 m/s on the platform. (a) Find the speed of A after he catches the ball for the first time. (c) Find the speeds of A and Bafter the all has made 5 round trips and is held by A. (d) How many times can A roll the ball? (e) Where is the centre of mass of the system "A + B + ball" at the end of the nth trip?
Solution
It is given that:
Weight of A = Weight of B = 40 kg
Velocity of ball = 5 m/s
(a) Case-1: Total momentum of the man A and ball remains constant.
∴ 0 = 4 × 5 − 40 × v
⇒ v = 0.5 m/s, towards left
(b) Case-2: When B catches the ball, the momentum between B and the ball remains constant.
⇒ 4 × 5 = 44 v
⇒ \[v = \left( \frac{20}{44} \right)\text{ m/s}\]
Case-3: When B throws the ball,
On applying the law of conservation of linear momentum, we get:
\[\Rightarrow 44 \times \left( \frac{20}{44} \right) = - 4 \times 5 + 40 \times v\]
\[ \Rightarrow v = 1 \text{ m/s , towards right)}\]
Case-4: When A catches the ball,
Applying the law of conservation of liner momentum, we get:
\[- 4 \times 5 + ( - 0 . 5) \times 40 = 44 v\]
\[ \Rightarrow v = \frac{40}{44} = \frac{10}{11}\text{ m/s, towards left}\]
(c) Case-5: When A throws the ball,
Applying the law of conservation of linear momentum, we get:
\[44 \times \left( \frac{10}{11} \right) = 4 \times 5 + 40 \times v\]
\[ \Rightarrow v = \frac{60}{40} = \frac{3}{2} \text{ m/s towards left)}\]
Case-6: When B receives the ball,
Applying the law of conservation of linear momentum, we get:
\[40 \times 1 + 4 \times 5 = 44 \times v\]
\[ \Rightarrow v = \frac{60}{44} \text{ m/s, towards right }\]
Case-7: When B throws the ball,
On applying the law of conservation of linear momentum, we get:
\[\Rightarrow v = 44 \times \left( \frac{60}{44} \right) \text{ m/s, towards right }\]
Case-8: When A catches the ball,
On applying the law of conservation of linear momentum, we get:
\[- 4 \times 5 + 40\left( \frac{3}{2} \right) = - 44v\]
\[ \Rightarrow V = - \frac{40}{44} = $\left( \frac{10}{11} \right) \text{ m/s,towards left } \]
Similarly, after 5 round trips,
The velocity of A will be \[\left( \frac{50}{11} \right)\] m/s and the velocity of B will be 5 m/s.
(d) As after 6 round trips, the velocity of A becomes \[\frac{60}{11}\] > 5 m/s, it cannot catch the ball. Thus, A can only roll the ball six times.
(e) Let the ball and the body A be at origin, in the initial position.
\[\therefore X_c = \frac{40 \times 0 + 4 \times 0 + 40 \times d}{40 + 40 + 4}\]
\[ = \frac{10}{21}d\]
APPEARS IN
RELATED QUESTIONS
If the linear momentum of a particle is known, can you find its kinetic energy? If the kinetic energy of a particle is know can you find its linear momentum?
Consider the situation of the previous problem. Take "the table plus the ball" as the system. friction between the table and the ball is then an internal force. As the ball slows down, the momentum of the system decreases. Which external force is responsible for this change in the momentum?
When a nucleus at rest emits a beta particle, it is found that the velocities of the recoiling nucleus and the beta particle are not along the same straight line. How can this be possible in view of the principle of conservation of momentum?
Consider the following two statements:
(A) Linear momentum of a system of particles is zero.
(B) Kinetic energy of a system of particles is zero.
A nucleus moving with a velocity \[\vec{v}\] emits an α-particle. Let the velocities of the α-particle and the remaining nucleus be v1 and v2 and their masses be m1 and m2.
A ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 45°. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball.
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum h/λ where h is the Planck's constant and λ is the wavelength of the light. A beam of light of wavelength λ is incident on a plane mirror at an angle of incidence θ. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
In a gamma decay process, the internal energy of a nucleus of mass M decreases, a gamma photon of energy E and linear momentum E/c is emitted and the nucleus recoils. Find the decrease in internal energy.
A block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s (In the following figure) towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

A bullet of mass 25 g is fired horizontally into a ballistic pendulum of mass 5.0 kg and gets embedded in it. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.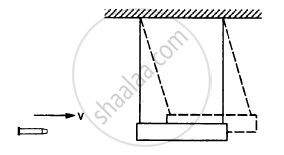
Two mass m1 and m2 are connected by a spring of spring constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
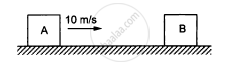
The blocks shown in figure have equal masses. The surface of A is smooth but that of Bhas a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic.
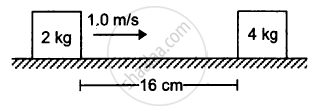
The friction coefficient between the horizontal surface and each of the block shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g = 10 m/s2.
A sphere starts rolling down an incline of inclination θ. Find the speed of its centre when it has covered a distance l.
The following figure shows a rough track, a portion of which is in the form of a cylinder of radius R. With what minimum linear speed should a sphere of radius r be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.

The following figure shows a small spherical ball of mass m rolling down the loop track. The ball is released on the linear portion at a vertical height H from the lowest point. The circular part shown has a radius R.
(a) Find the kinetic energy of the ball when it is at a point A where the radius makes an angle θ with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at A.
(c) Find the normal force and the frictional force acting on the if ball if H = 60 cm, R = 10 cm, θ = 0 and m = 70 g.

A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
The track shown is figure is frictionless. The block B of mass 2m is lying at rest and the block A or mass m is pushed along the track with some speed. The collision between Aand B is perfectly elastic. With what velocity should the block A be started to get the sleeping man awakened?

