Question

A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.

Answer 1

According to the question, the surface is frictionless. Thus, the block m will slide down the inclined plane of mass M.
Acceleration, a₁ = g sin α        (Relative to the inclined plane)

The horizontal component of acceleration a₁ is given by a_x =  g sin α cos α, for which the block M accelerates towards left.
Let the left acceleration be a₂.

By the concept of centre of mass, we can say that the external force is zero in the horizontal direction. 
\[m a_x  =   (M + m) a_2\]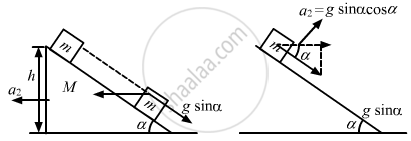


Absolute (resultant) acceleration of m on the plane M, along the direction of the incline will be = \[a =   g  \sin  \alpha -    a_2   \cos  \alpha\] 
Let the time taken by the block m to reach the bottom end be t.

Now,

\[s = ut + \left( \frac{1}{2} \right)a t^2 \] 

\[ \Rightarrow   \frac{h}{\sin  \alpha} = \left( \frac{1}{2} \right)a t^2 \] 

\[ \Rightarrow   t = \sqrt{\frac{2h}{a  \sin  \alpha}}\]
Thus, the velocity of the bigger block after time t will be,

\[v_m  = u =  a_2 t\] 

\[ = \frac{mg  \sin  \alpha  \cos  \alpha}{M + m}  \sqrt{\frac{2h}{a  \sin  \alpha}} =  \left[ \frac{2 m^2 g^2 h  \sin^2 \alpha  \cos^2 \alpha}{(M + m )^2 a  \sin  \alpha} \right]^{1/2}\]
Subtracting the value of a from equation (2), we get:
\[v_M  =   \left[ \frac{2 m^2 g^2 h  \sin^2 \alpha}{(M + m )^2 \sin  \alpha} \times \frac{\cos^2 \alpha}{g  \sin  \alpha}  \frac{(M + m)}{(M + m  \sin^2 \alpha)} \right]\]