Advertisements
Advertisements
प्रश्न
A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision, what could be the minimum and the maximum value of u.
उत्तर
It is given that:
Mass of particles = 100 g
Initial speed of the first particle = u
Final K.E. of the system after collision = 0.2J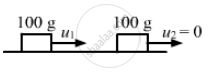
Initial K.E. of the system, before collision = \[\frac{1}{2}m u^2 + 0 \]
i.e. Initial K.E. = \[\frac{1}{2} \times 0 . 1 \times u^2 = 0 . 05 u^2\]
Let v1 and v2 be the final velocities of the first and second block respectively.
Let v1 and v2 be the final velocities of the first and second block respectively.
By law of conservation of momentum, we know:
\[m v_1 + m v_2 = mu\]
\[\Rightarrow v_1 + v_2 = u . . . (1)\]
\[( v_1 - v_2 ) + e( u_1 - u_2 ) = 0\]
\[ \Rightarrow eu = v_2 - v_1 . . . (2) [\text{ Putting } u_2 = 0, u_1 = u]\]
\[\text{ Adding the equations (1) and (2), we get:}\]
\[ 2 v_2 = (1 + e)u\]
\[ \Rightarrow v_2 = \left( \frac{u}{2} \right)(1 + e)\]
\[ \therefore v_1 = u - \frac{u}{2}(1 + e)\]
\[ v_1 = \frac{u}{2}(1 - e)\]
\[\text{ According to given condition, }\]
\[\frac{1}{2}m v_1^2 + \frac{1}{2}m v_2^2 = 0 . 2\]
\[ \Rightarrow v_1^2 + v_2^2 = 4\]
\[ \Rightarrow \frac{u^2}{2}\left( 1 + e^2 \right) = 4\]
\[ \Rightarrow u^2 = \frac{8}{1 + e^2}\]
For maximum value of u, denominator should be minimum in the above equation.
i.e. e = 0
⇒ u2 = 8
\[\Rightarrow u = 2\sqrt{2} \text{ m/s}\]
For minimum value of u, denominator should have maximum value.
i.e. e = 1
⇒ u2 = 4
⇒ u = 2 m/s .
APPEARS IN
संबंधित प्रश्न
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
Consider the following the equations
(A) \[\vec{R} = \frac{1}{M} \sum_i m_i \vec{r_i}\] and
(B) \[\vec{a}_{CM} = \frac{\vec{F}}{M}\]
In a noninertial frame
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
In which of the following cases the centre of mass of a rod is certainly not at its centre?
(a) the density continuously increases from left to right
(b) the density continuously decreases from left to right
(c) the density decreases from left to right upto the centre and then increases
(d) the density increases from left to right upto the centre and then decreases.
A nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to be v0 and a0 at instant t. It is possible that
(a) v0 = 0, a0 = 0
(b) v0 = 0, a0 ≠ 0
(c) v0 ≠ 0, a0 = 0
(d) v0 ≠ 0, a0 ≠ 0
Three particles of masses 1.0 kg, 2.0 kg and 3.0 kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1 m. Locate the centre of mass of the system.
Seven homogeneous bricks, each of length L, are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L/10. Find the x-coordinate fo the centre of mass relative to the origin shown.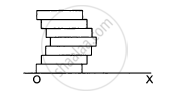
The balloon, the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distance does the balloon descend? Mass of the balloon = M, mass of the monkey = m and the length of the rope ascended by the monkey = L.

A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
Consider the situation of the previous problem. Suppose each of the blocks is pulled by a constant force F instead of any impulse. Find the maximum elongation that the spring will suffer and the distance moved by the two blocks in the process.
Consider the situation of the previous problem. Suppose the block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2. Find the maximum elongation that the spring will suffer.
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
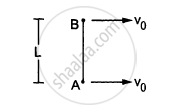
[Hint : The light rod will exert a force on the ball B
only along its length.]
Solve the following problem.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the center of the sphere while the other is at the boundary. Locate center of mass of the remaining sphere.
In system of two particles of masses 'm1' and 'm2', the first particle is moved by a distance 'd' towards the centre of mass. To keep the centre of mass unchanged, the second particle will have to be moved by a distance ______.
The ratio of weights of a man inside a lift when it is stationary and when it is going down with a uniform acceleration 'a' is 3 : 2. The value of 'a' will be ______.
(a< g, g = acceleration due to gravity)
Centre of mass is a point ______.
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
